Proporção
Definição, significado, elementos e propriedades, aprenda tudo isso e muito mais sobre uma proporção. Veja exemplos de como utilizar a propriedade fundamental!
Quando duas razões são iguais, dizemos que elas formam uma proporção. Em outras palavras, considerando quatro números racionais, ,
,
e
, diferentes de zero, temos uma proporção quando:
Lê-se: está para
, assim como
está para
.
Significado de proporção
Para entender o significado de uma proporção, considere o seguinte exemplo:
Na embalagem de um suco concentrado diz que, para preparar a bebida, basta acrescentar 1 copo de suco para cada 5 copos de água.
Dessa forma, a razão entre a quantidade de suco e água é de 1 para 5, ou seja, .
Então, para 10 copos de água, devem ser colocados 2 copos de suco. Nesse caso, a razão entre a quantidade de suco e água é de 2 para 10, ou seja, .
Observe que, embora os números que formam as razões sejam diferentes, a quantidade de suco aumentou na mesma medida que a água, ambas dobraram, isto é, as quantidades são proporcionais:
Veja ainda que, e que
.
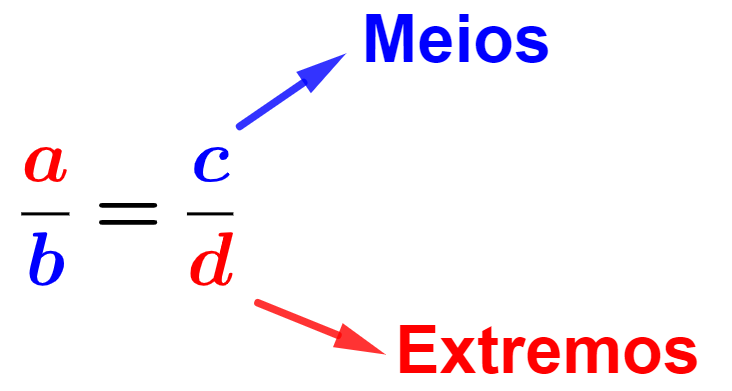
Elementos de uma proporção
Os números que formam uma proporção são chamados de termos. Os termos e
são chamados de extremos e os termos
e
são os meios.
Propriedade fundamental das proporções
Em toda proporção, o produto dos extremos deve ser igual ao produto dos meios, isto é:
Essa propriedade é conhecida como propriedade fundamental das proporções.
Exemplo 1: Verifique se as razões a seguir formam uma proporção:
a) e
Produto dos extremos: 3 . 24 = 72
Produto dos meios: 9 . 8 = 72
Os produtos são iguais, 72 = 72, então, as razões formam uma proporção:
b) e
Produto dos extremos: 2 . 12 = 24
Produto dos meios: 4 . 3 = 12
Os produtos não são iguais, 24 12, então, as razões não formam uma proporção.
Exemplo 2: Encontre o valor de x em .
Se temos uma igualdade entre duas razões, então, temos uma proporção.
Pela propriedade fundamental das proporções, temos que:
15 . x = 6 . 5
⇒ 15 . x = 30
⇒ x = 30/15
⇒ x = 2
Outras propriedades da proporção
Além da propriedade fundamental, existem outras duas propriedades da proporção.
Propriedade 1. Se , então, as seguintes igualdades são verdadeiras:
Propriedade 2. Se , então, as seguintes igualdades são verdadeiras:
Você também pode se interessar:
- Grandezas diretamente e inversamente proporcionais
- Exercícios sobre razão e proporção
- Regra de três – Veja os tipos e aprenda como calcular
- Números decimais e porcentagem


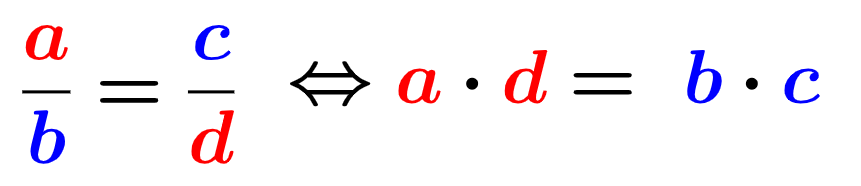
Os comentários estão fechados, mas trackbacks E pingbacks estão abertos.