Retas concorrentes

Em geometria plana, retas concorrentes são duas retas que possuem um único ponto em comum.

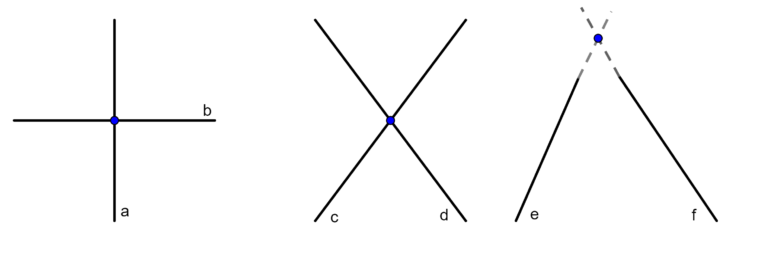
Exemplos de retas concorrentes:

Observe que, se duas retas são concorrentes, a inclinação de cada uma é diferente, por isso elas sempre se cruzam em um ponto.

Outro detalhe importante é que as retas são infinitas, então, mesmo que o ponto de intersecção entre as retas não seja “evidente” na representação, como ocorre com as retas e e f, isso não significa que não sejam retas concorrentes.

Tipos de retas concorrentes

No ponto de cruzamento entre duas retas concorrentes sempre são formados quatro ângulos, que somam 360°, ou seja, uma volta completa.

De acordo com as medidas desses ângulos, as retas concorrentes podem ser de dois tipos diferentes.

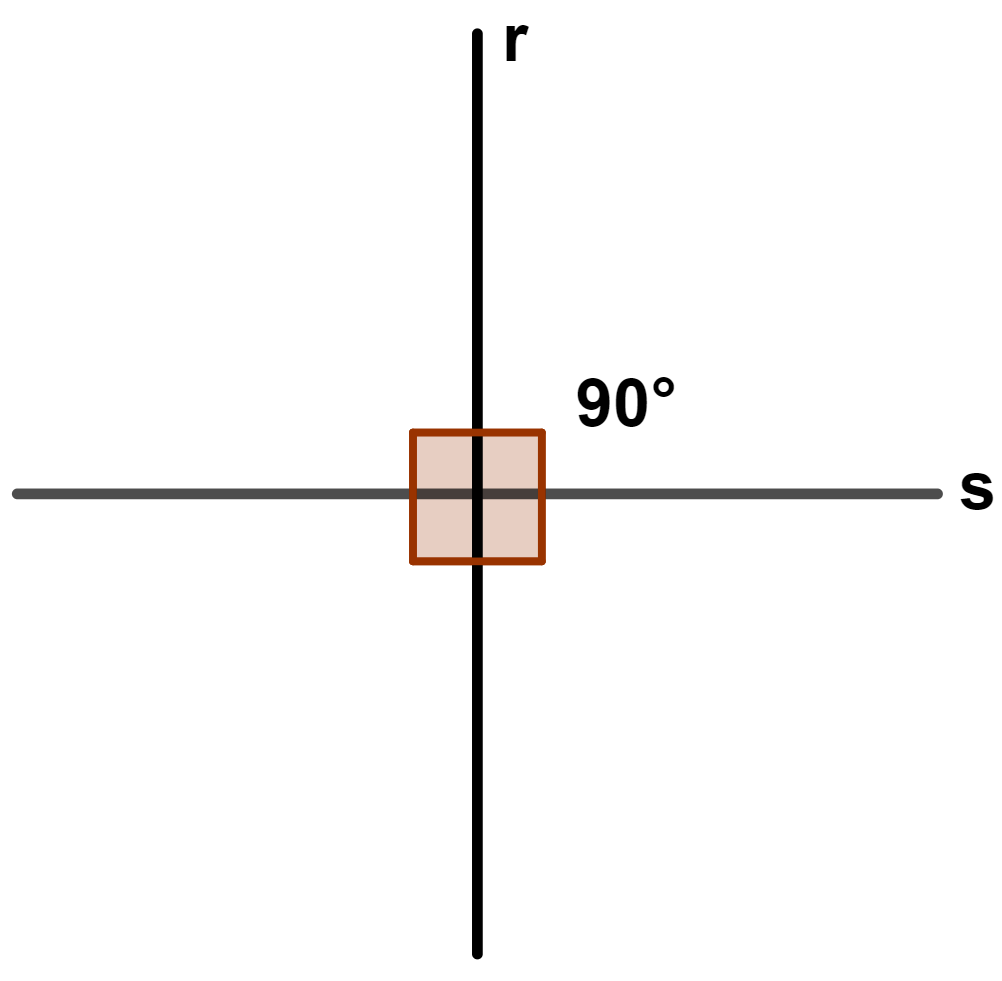
Retas concorrentes perpendiculares

Quando os ângulos têm a mesma medida, formando quatro ângulos retos (90°), as retas concorrentes são perpendiculares.

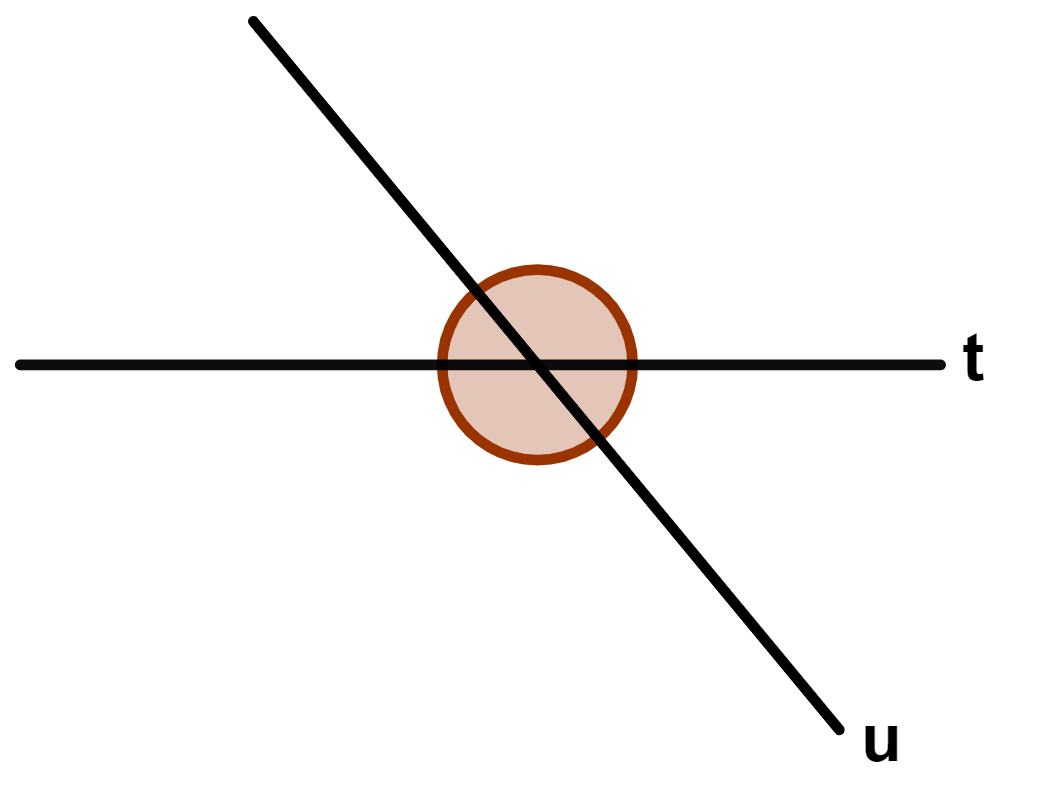
Retas concorrentes oblíquas

Quando os ângulos têm medidas diferentes, as retas concorrentes são oblíquas.

Ângulos opostos pelo vértice

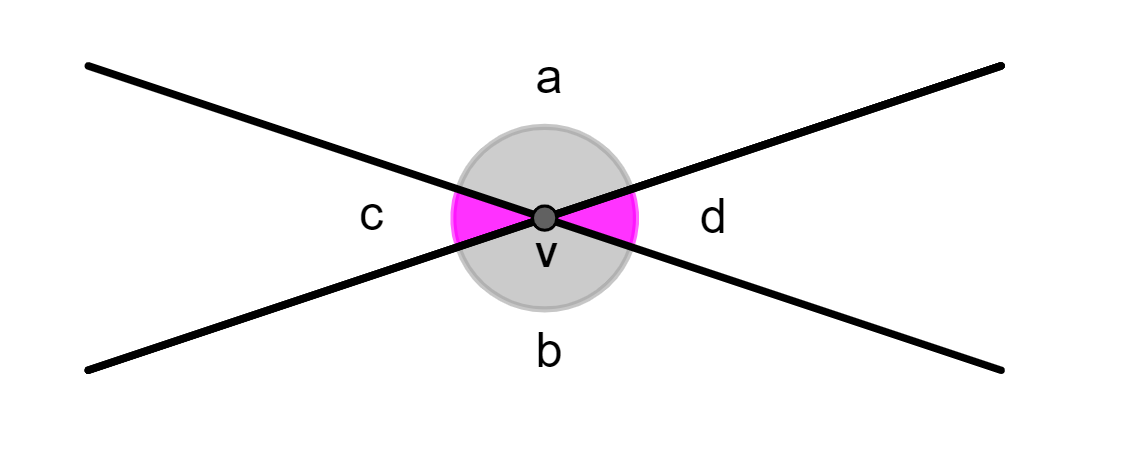
Chamando de vértice o ponto de encontro entre duas retas concorrentes, podemos identificar os ângulos opostos pelo vértice.

Na figura, os ângulos a e b e os ângulos c e d são opostos pelo vértice.

Uma propriedade dos ângulos opostos pelo vértice é que eles são congruentes, isto é, têm a mesma medida. Assim:

• a = b
• c = d

Essas relações são muito úteis para determinar medidas desconhecidas de ângulos formados por duas retas concorrentes.

Intersecção entre duas retas concorrentes

O ponto de intersecção entre duas retas concorrentes pode ser determinado a partir das equações das retas.

As retas se cruzam em um ponto que pertence às duas retas, ou seja, o ponto que satisfaz às duas equações.

Assim, para determinar qual é esse ponto, basta resolver o sistema de equações formado pelas equações das duas retas.

Exemplo: encontrar o ponto de intersecção entre as retas  e .

Para encontrar o ponto basta resolver o seguinte sistema:

• Da 1ª equação, temos que: .
• Substituindo  na 2ª equação, temos: 
• Resolvendo essa equação, obtemos: 
• Substituindo  por 3,8 em , encontramos .

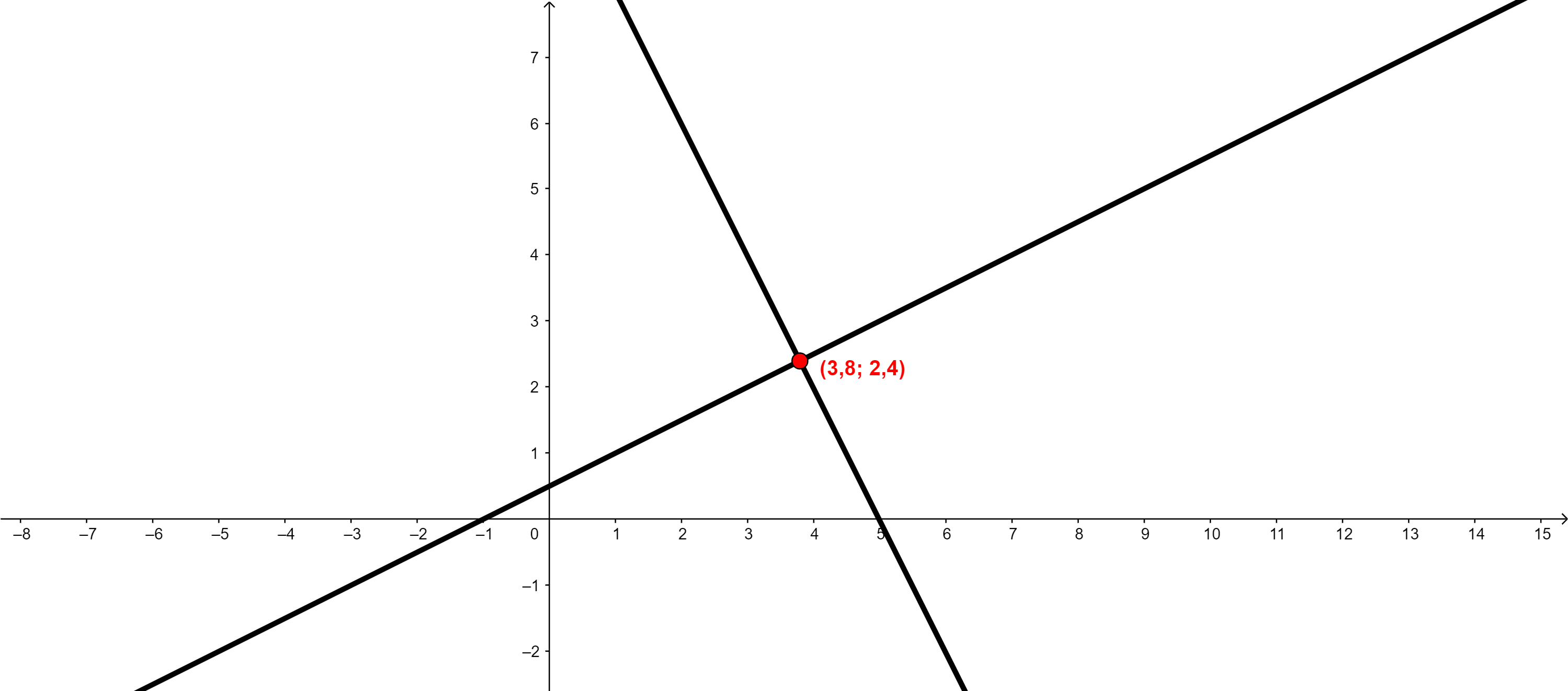
Portanto, o ponto de intersecção entre as retas é o ponto (x; y) = (3,8 ; 2,4).

Veja a representação no sistema de coordenadas:

Você também pode se interessar:

• Equação da reta
• Reta, semirreta e segmento de reta
• Método prático para resolver equações do 1° grau