Sistemas de equações
Aprenda dois diferentes métodos para resolver um sistema de equações e saiba como classificar um sistema em possível determinado, possível indeterminado e impossível.
Um sistema de equações é um sistema matemático formado por equações que possuem mais de uma incógnita e que estão relacionadas a uma mesma situação.
Assim, devemos resolver as equações simultaneamente, encontrando valores para as incógnitas que satisfaçam todas as equações do sistema.
Quando cada equação do sistema é uma equação do 1º grau, temos um sistema de equações do 1º grau.
Exemplo de sistema de equações do 1º grau
Em um estacionamento o número de carros, mais o número de motos, é igual a 25, e o número de carros, menos o número de motos, é igual a 5. Quantos carros e quantas motos tem nesse estacionamento?
- Incógnita x: representa o número de carros;
- Incógnita y: representa o número de motos.
Equações relacionadas a esse problema:
e
Sistema de equações:
Como resolver esse sistema e encontrar os valores de x e de y? Vamos ver!
Como resolver um sistema de equações do 1º grau?
Vamos mostrar dois métodos para resolver um sistema de equações do 1º grau: método da substituição e método da adição.
- Método da substituição
O método da substituição consiste em isolar uma das incógnitas em uma equação e depois substituir o valor na outra equação. Após isso, encontramos o valor de cada uma das incógnitas.
Exemplo: Vamos resolver o sistema do problema do estacionamento pelo método da substituição.
1º passo: Escolhemos uma das equações do sistema, preferencialmente a que for mais simples, e então isolamos a incógnita x.
2º passo: Substituímos o valor de x na outra equação e resolvemos para encontrar o valor de y.
3º passo: Substituímos y por 10 em , para encontrar o valor de x.
Logo, x = 15 e y = 10. Assim, a solução do sistema é o par ordenado (15, 10). Significa que tem 15 carros e 10 motos no estacionamento.
- Método da adição
O método da adição consiste em somar as equações, membro a membro, para fazer “sumir” uma das incógnitas e encontrar o valor da outra incógnita.
Exemplo: Vamos resolver o sistema do problema do estacionamento pelo método da adição.
1º passo: Na primeira equação temos +y e na segunda equação temos -y, que são termos opostos. Então, vamos somar as duas equações para “sumir” com a incógnita y e encontrar o valor de x.
2º passo: Substituímos x por 15 em qualquer uma das equações para encontrar o valor de y.
Pronto! Chegamos na solução do sistema: par ordenado (15, 10). Vamos ver mais um exemplo.
Exemplo: Resolver o sistema abaixo pelo método da adição.
Se somarmos as equações nenhuma das incógnitas irá sumir, pois não temos termos opostos. Então, antes de somarmos, vamos multiplicar as equações de modo que apareçam termos opostos.
1º Passo:
- Multiplicamos todos os membros da 1º equação por 2;
- Multiplicamos todos os membros da 2º equação por 3.
2º Passo: Agora, na primeira equação temos +6y e na segunda equação temos -6y, que são termos opostos . Então, vamos somar as duas equações para “sumir” com a incógnita y e encontrar o valor de x.
3º passo: Substituímos x por 1 em qualquer uma das equações para encontrar o valor de y.
Logo, x = 1 e y = -1. Assim, a solução do sistema é o par ordenado (1, -1).
Classificação dos sistemas de equações
Ao resolver sistemas de equações, podemos encontrar uma única solução, infinitas soluções ou nenhuma solução.
Nesse sentido, podemos classificar os sistemas em sistema possível determinado, sistema possível indeterminado ou sistema impossível.
- Sistema possível determinado
Um sistema possível determinado possui uma única solução.
Exemplo:
Esse sistema possui uma única solução, que é o par ordenado (15, 7).
- Sistema possível indeterminado
Um sistema possível indeterminado possui infinitas soluções.
Exemplo:
Esse sistema possui infinitas soluções, por exemplo, os pares ordenados (1, 1), (0, 2) e (2, 0).
- Sistema impossível
Um sistema impossível não possui solução.
Exemplo:
Esse sistema não possui nenhuma solução, pois não existe nenhum par ordenado (x, y) que satisfaça as duas equações ao mesmo tempo.
Você também pode se interessar:

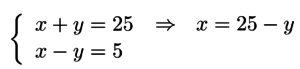
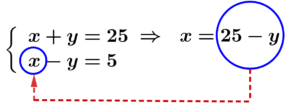
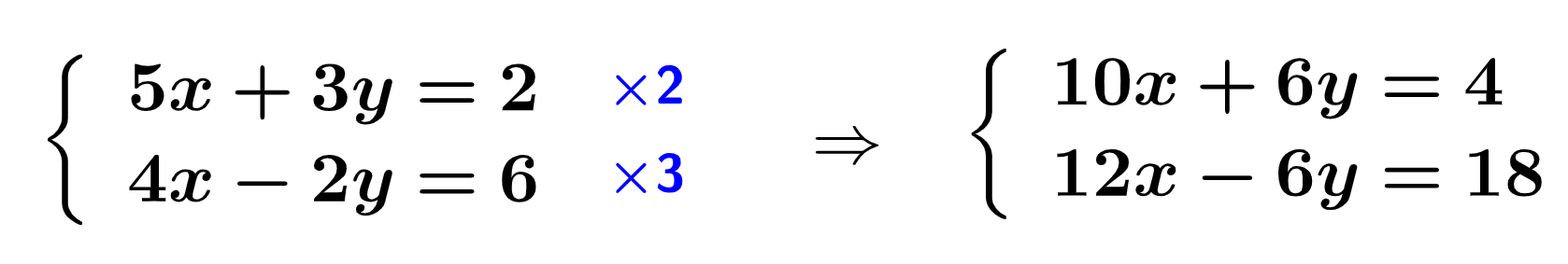
Os comentários estão fechados, mas trackbacks E pingbacks estão abertos.