Tronco de cone

O tronco de cone corresponde à parte inferior do cone sem o vértice. Aprenda a calcular a área e volume desse tipo de figura espacial.

Por Elainy Marciano Publicado em 19/11/2020 - 17:43

O tronco de cone é a parte inferior de um cone, a parte sem o vértice. O tronco de cone é obtido quando o cone é cortado por um plano paralelo ao plano da sua base circular.

Veja mais

O limite numérico: até onde vai o maior número que conhecemos?

Reditec debate ensino profissional e tecnológico

Portanto, o tronco de cone é, também, um sólido geométrico, e nesse tipo de figura podemos calcular a área da sua superfície e o seu volume ou capacidade. Mas, antes disso, precisamos conhecer os elementos do tronco de cone.

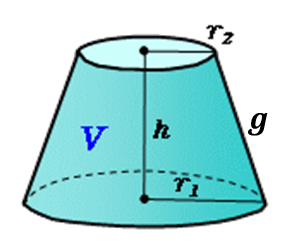
Observe, na figura, que o tronco de cone possui duas bases circulares, uma maior e outra menor. A base maior corresponde à base do cone com raio $\dpi{120} \boldsymbol{r_1}$ e a base menor, de raio $\dpi{120} \boldsymbol{r_2}$ , é a base obtida com o corte feito pelo plano.

A medida do segmento $\dpi{120} \boldsymbol{h}$ que liga o centro das bases é a altura do tronco de cone. Já a medida da lateral do tronco de cone é a sua geratriz $\dpi{120} \boldsymbol{g}$ .

Área do tronco de cone

A área de um sólido geométrico nada mais é do que a medida da sua superfície, ou seja, da parte externa que forma a figura.

A área do tronco de cone pode ser calculada a partir da seguinte fórmula:

$\dpi{120} \boldsymbol{A = \pi \cdot g\cdot (r_1 + r_2)}$

Em que:

$\dpi{120} \boldsymbol{g}$ : geratriz do tronco de cone;
$\dpi{120} \boldsymbol{r_1}$ : raio da base maior;
$\dpi{120} \boldsymbol{r_2}$ : raio da base menor.

Exemplo:

Um cone com 8 centímetros de raio foi cortado, obtendo-se um tronco de cone com geratriz igual a 6 centímetros e raio da base menor igual a 5 centímetros. Determine a área da superfície desse tronco de cone.

$\dpi{120} {A = \pi \cdot 6\cdot (8 + 5)}$