Sólidos geométricos
Sólidos geométricos são figuras espaciais. Saiba quais são as classificações, características, fórmulas de volume e muito mais!
Os sólidos geométricos são figuras tridimensionais que possuem altura, largura e comprimento. Eles são estudados pela Geometria Espacial e se subdividem em dois grupos: poliedros e corpos redondos.
Poliedros
Os poliedros são sólidos geométricos formados por faces, arestas e vértices, cujas faces são apenas figuras geométricas planas.
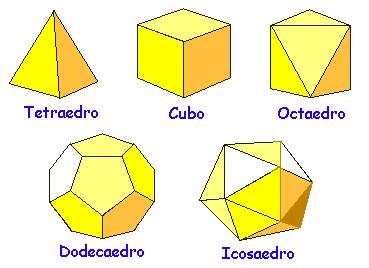
As faces são cada um dos lados que formam o poliedro, podendo ser triângulos, quadriláteros, pentágonos, etc. As arestas são os segmentos de reta que formam a figura. Por fim, os vértices são os pontos de encontro entre as arestas.
Os poliedros podem ser classificados em poliedros convexos e poliedros côncavos (não convexos), que são aqueles em que podemos observar uma concavidade na figura.
Além disso, entre os poliedros, há alguns tipos específicos, que reúnem características semelhantes. Vamos conhecê-los?
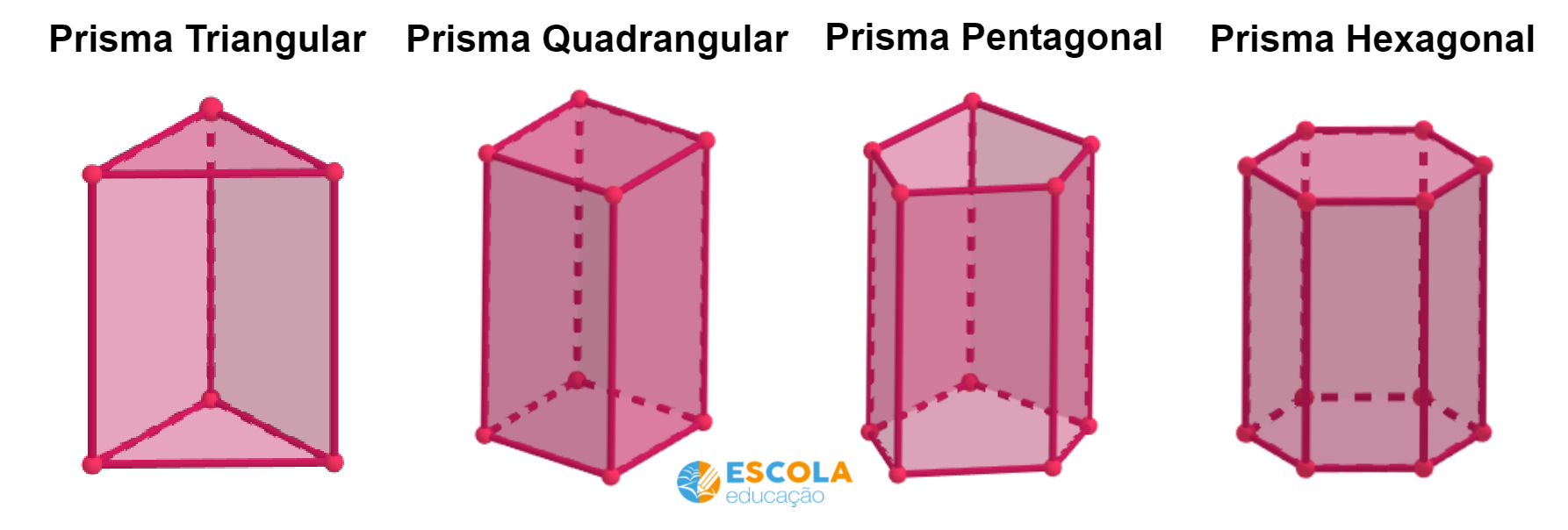
Prismas
Os prismas são poliedros que possuem duas faces que estão em planos paralelos e são chamadas de bases, e as outras faces são faces laterais.
Veja alguns exemplos de prismas:
Volume do prisma:
: área da base;
: altura.
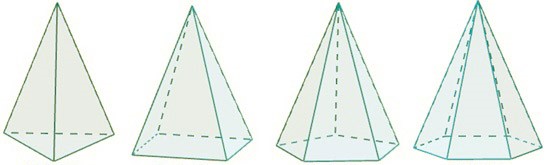
Pirâmides
As pirâmides são poliedros que possuem um polígono como base e apenas um vértice localizado em um plano diferente do plano da base.
Volume da pirâmide:
: área da base;
: altura.
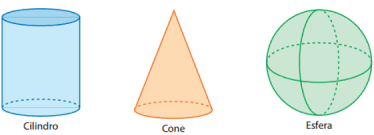
Corpos redondos
Os corpos redondos (ou não poliedros) são os sólidos geométricos arredondados, como cilindros, cones, e esferas.
Volume do cilindro:
: raio da base;
: altura.
Volume do cone:
: raio da base;
: altura.
Volume da esfera:
Você também pode se interessar:
- Cubo
- Paralelepípedo
- Planificação de sólidos geométricos
- Medidas de volume e capacidade
- Lista de exercícios de área de figuras planas

Os comentários estão fechados, mas trackbacks E pingbacks estão abertos.