Volume da pirâmide
O volume da pirâmide é uma medida que depende da sua base. Entenda mais sobre isso e veja exemplos de como calcular o volume da pirâmide.
A pirâmide é uma figura geométrica espacial, e nesse tipo de figura, podemos calcular o volume. O volume nada mais é do que a capacidade de um sólido geométrico.
Existem alguns tipos de pirâmides e para entender como calcular o volume, é necessário entender como elas são formadas e qual a diferença entre elas.
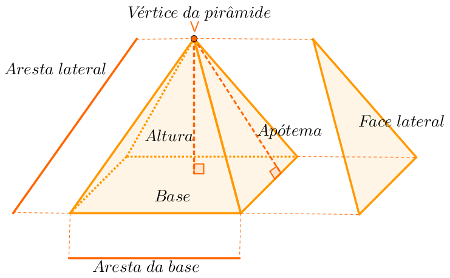
Elementos da pirâmide
Considere um polígono em um plano e um ponto contido em outro plano. As pirâmides são as figuras formadas por todos os segmentos de reta que ligam o ponto ao polígono.
O polígono é chamado de base e o ponto é o vértice da pirâmide.
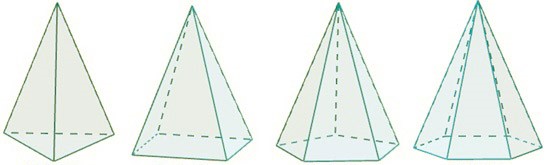
Tipos de pirâmides
A base de uma pirâmide pode ser um triângulo, retângulo, pentágono, hexágono, entre outros polígonos.
Veja alguns exemplos de pirâmides:
Como calcular o volume da pirâmide
O volume da pirâmide é uma medida que depende da área da base e da altura:
: área da base;
- H: altura da pirâmide.
Dessa forma, para cada tipo de pirâmide, o volume poderá ter uma fórmula diferente. Veja, por exemplo, o volume de uma pirâmide triangular.
Volume da pirâmide triangular:
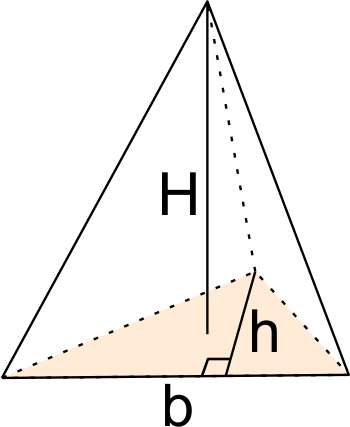
Exemplo: vamos calcular o volume de uma pirâmide de altura 12 cm e base com as seguintes medidas: b = 8 cm e h = 5 cm.
Portanto, o volume é igual a 80 cm³.
Você também pode se interessar:

Os comentários estão fechados, mas trackbacks E pingbacks estão abertos.