Primeiramente, o que é o algoritmo da divisão? O algoritmo da divisão é, simplesmente, o passo a passo para resolver uma conta de divisão, que apesar de ser uma das quatro operações básicas da matemática, costuma ser temida por muitos estudantes.
Por isso temos uma dica importante: Saber a tabuada de multiplicação é essencial para fazer contas de dividir, já que essas duas operações são inversas. Então, se você ainda tem dificuldades com essa tabuada, dá uma conferida nesse post: tabuada de multiplicação.
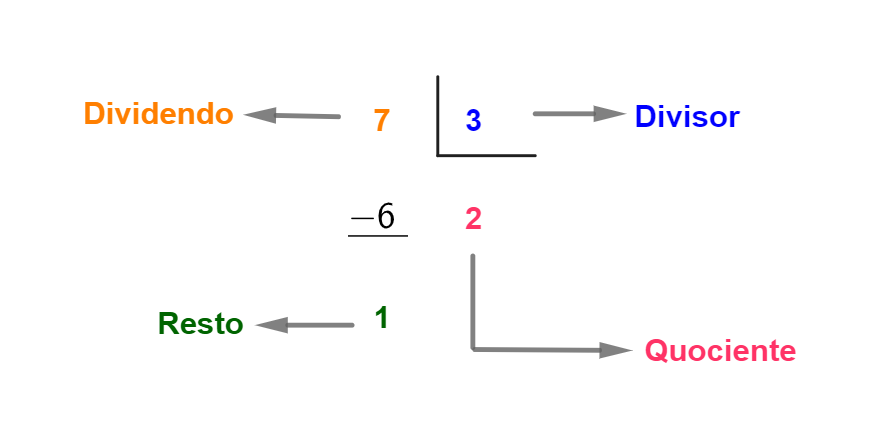
Dito isso, vamos recordar que os elementos de uma divisão são: dividendo, divisor, quociente e resto.
Agora, vamos para o passo a passo, resolvendo alguns exemplos.
Exemplo 1
Fazer 7 dividido por 3, que também pode ser escrito como 7 3 ou 7 : 3, ou ainda, 7/3 .
Passo 1. Identificar o dividendo e o divisor
O número 7 é o nosso dividendo, ou seja, o número que queremos dividir. Já o número 3, é o divisor, o número que vai dentro da chave na divisão.
Passo 2. Encontrar o quociente
O quociente é um número natural que, ao ser multiplicado pelo divisor, o resultado é igual ao dividendo ou a um número um pouco menor que o dividendo.
Vamos recordar a tabuada do 3, que é o divisor:
3 x 0 = 0 3 x 1 = 3 3 x 2 = 6 3 x 3 = 9 3 x 4 = 12
Conclusão: não existe nenhum número natural que, multiplicado por 3, resulte 7.
Então o que devemos fazer? Vamos procurar um número que, ao ser multiplicado por 3, tenha um resultado menor que 7.
Temos: 3 x 0 = 0 3 x 1 = 3 3 x 2 = 6
Então, os números que resultam em um valor menor que 7 são: 0, 1 e 2.
Qual deles vamos considerar? Vamos considerar o que nos resulta no valor mais próximo de 7, que neste caso é o 2, com resultado igual a 6.
Logo, o número 2 é nosso quociente, ele é colocado embaixo da chave.
Passo 3. Calcular o resto
O resto é o resultado da subtração entre o dividendo e o produto do quociente pelo divisor.
Produto: 3 x 2 = 6
Subtração: 7 – 6 = 1
Então, o resto é igual a 1, é o que sobrou na divisão.
Finalizamos a conta!
Agora, observe que se multiplicarmos o divisor pelo quociente e, ao resultado, somarmos o resto, obtemos o dividendo:
3 x 2 + 1 = 6 + 1 = 7
Isso significa que a nossa conta está correta, pois em uma divisão sempre vamos ter:
Dividendo = quociente x divisor + resto
Se o resto da divisão for igual a 0, se reduz a:
Dividendo = quociente x divisor
Exemplo 2
Fazer 68 dividido por 4.
Passo 1. Identificar o dividendo e o divisor
O número 68 é o nosso dividendo e o número 4 é o divisor, ou seja, é o número que vai dentro da chave na divisão.
Passo 2. Encontrar o quociente
O quociente é um número natural que, ao ser multiplicado pelo divisor, o resultado é igual ao dividendo ou a um número um pouco menor que o dividendo.
Podemos testar vários números até encontrar um que, ao multiplicar por 4, o resultado seja 68. Mas, temos uma maneira mais prática de resolver isso, veja:
O dividendo, 68, tem dois algarismos. O primeiro algarismo é 6, que é maior que o divisor 4. Então, o que vamos fazer é esquecer um pouco do segundo algarismo e resolver a conta em duas etapas.
Primeira etapa: a conta que temos que resolver é apenas 6 dividido por 4, isto é, 6 4:
Não tem nenhum número que, ao ser multiplicado por 4, o resultado seja 6. Procurando um número menor, temos que o quociente é 1, pois 4 x 1 = 4 (resultado mais próximo de 6). Então, o 1 é colocado embaixo da chave.
Depois disso, calculamos o resto, fazendo a subtração: 6 – 4 = 2.
O resto é 2. Agora, vamos para a segunda etapa.
Segunda etapa: voltamos ao nosso dividendo considerando o segundo algarismo, que é o 8. O que fazemos com ele? Descemos. Colocamos o 8 ao lado do número 2. Assim, temos um número formado: 28.
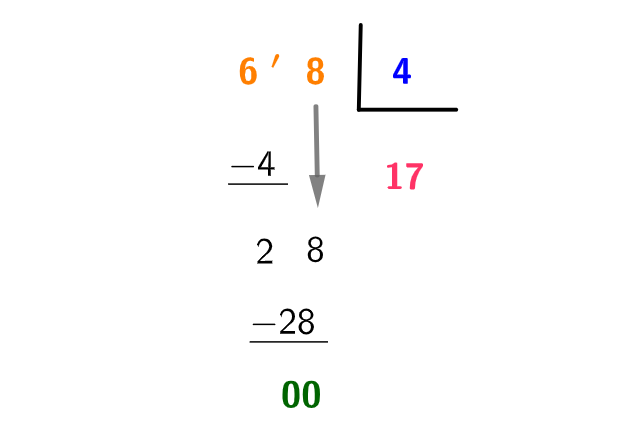
O 28 passa a ser nosso dividendo, vamos dividir 28 por 4, ou seja, 28 4:
Temos que 7 x 4 = 28. Então, nessa conta, o quociente é 7. Colocamos o 7 na chave ao lado do 1.
Como não temos nenhum outro algarismo do dividendo para descer, então finalizamos essa etapa: o quociente é igual a 17.
Passo 3. Calcular o resto:
Produto: 17 x 4 = 28
Subtração: 28 – 28 = 0.
O resto é igual a 0.
Finalizamos a conta!
Você também pode se interessar:
- Tabuada de divisão – Uso no dia a dia e benefícios em aprender
- Múltiplos e divisores – O que são e como encontrar
- Atividades de divisão para imprimir – 3º ano

Os comentários estão fechados, mas trackbacks E pingbacks estão abertos.