Ângulos no círculo

Ângulo central, ângulo inscrito e ângulos excêntricos internos e externos, entenda o que são cada um desses tipos e suas propriedades!

Por Elainy Marciano Publicado em 02/12/2020 - 16:45

O estudo dos ângulos no círculo e circunferência constitui uma parte importante na geometria plana, já que essas figuras geométricas estão presentes em muitos objetos do dia a dia.

Considere, por exemplo, uma roda de bicicleta. A roda de uma bicicleta tem formato de um círculo, o seu aro é uma circunferência, e o encontro entre duas hastes quaisquer no interior da roda forma diversos ângulos.

Veja mais

O limite numérico: até onde vai o maior número que conhecemos?

Reditec debate ensino profissional e tecnológico

Os ângulos no círculo (ou circunferência) podem ser: centrais, inscritos, excêntricos internos ou excêntricos externos. Entenda cada um desses tipos!

Ângulo central

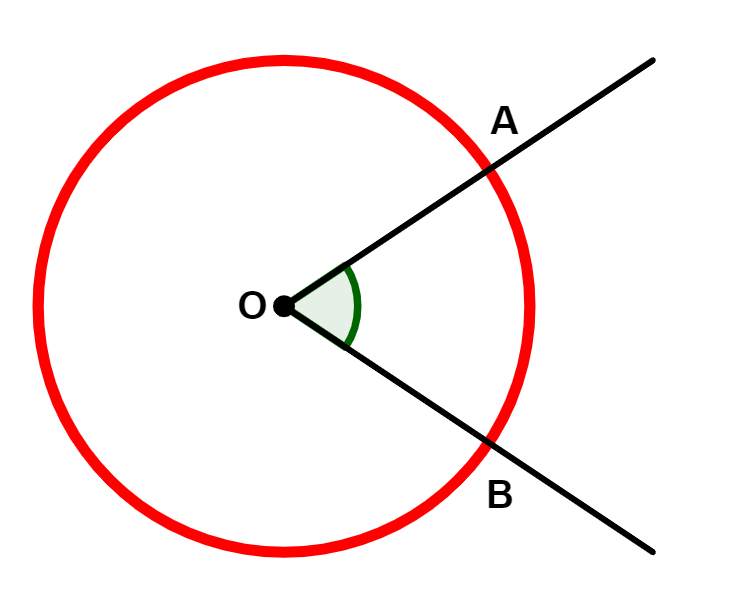
Em um círculo, um ângulo é chamado de ângulo central quando o seu vértice está no centro da circunferência do círculo.

Na figura acima, o ângulo $\small \mathrm{A\widehat{O}B}$ é um ângulo central.

Nesse tipo de ângulo, a medida do arco menor é igual à medida do ângulo central, ou seja:

$\small \mathbf{ Medida(A\widehat{O}B)= \widehat{AB} }$

Já a medida do arco maior, é obtida calculando-se a diferença entre a medida da volta completa (360°) e a medida do ângulo central.

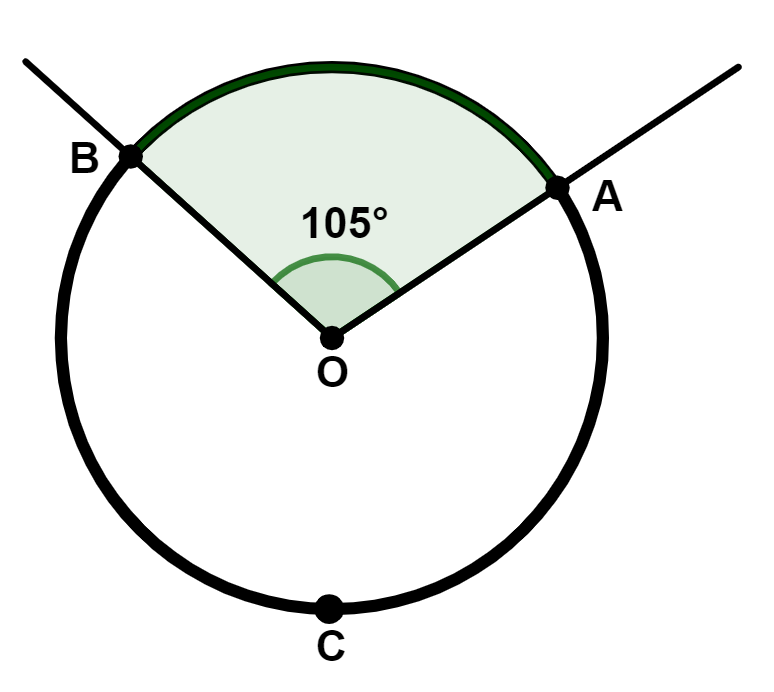
Exemplo: Determine a medida do arco menor $\dpi{100} \small \mathrm{\widehat{AB}}$ e do arco maior $\dpi{100} \small \mathrm{\widehat{ACB}}$ na figura abaixo:

O arco menor mede 105° e o arco maior mede 360° – 105° = 255°.

Ângulo inscrito

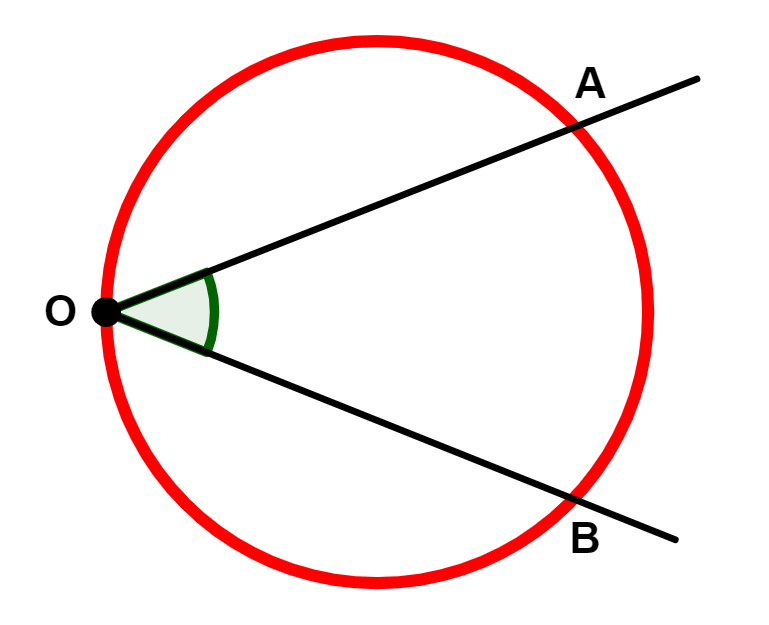
Um ângulo cujo vértice é um ponto da circunferência do círculo é chamado de ângulo inscrito.

Na figura acima, o ângulo $\small \mathrm{A\widehat{O}B}$ é um ângulo inscrito.

A medida de um ângulo inscrito é igual à metade da medida do ângulo central correspondente, ou seja, aquele cujo vértice está no centro da circunferência e os seus lados também passam pelos pontos A e B.

Lembrando que o ângulo central tem a mesma medida do arco menor $\dpi{100} \small \mathrm{\widehat{AB}}$ , temos que a medida do ângulo inscrito $\small \mathrm{A\widehat{O}B}$ é dada por:

$\small \mathbf{Medida(A\widehat{O}B) = \frac{Medida \, de \, \widehat{AB}}{2}}$

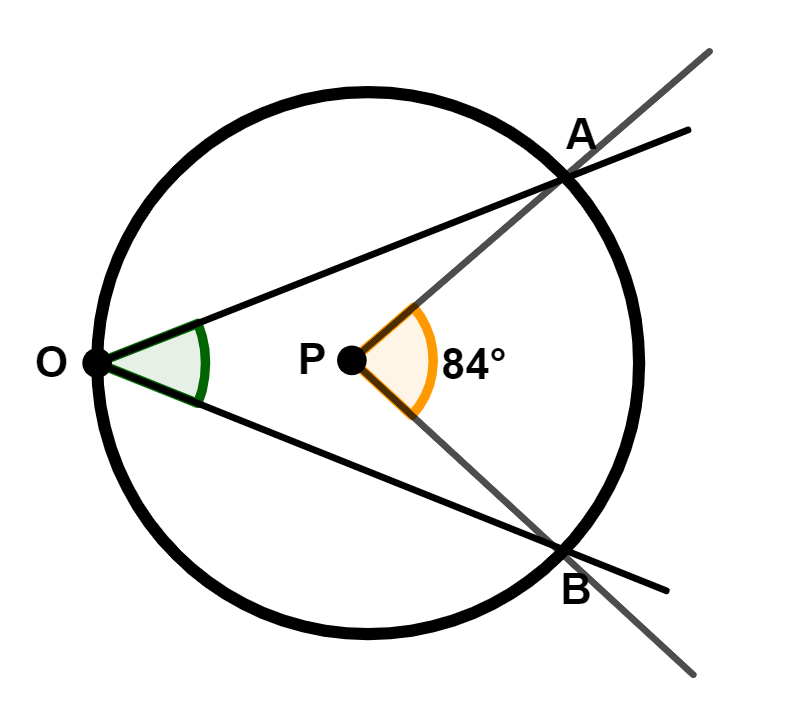
Exemplo: Determine a medida do ângulo inscrito $\small \mathrm{A\widehat{O}B}$ na figura abaixo:

Podemos ver que a medida do ângulo central correspondente $\small \mathrm{A\widehat{P}B}$ é 84°. Logo, a medida do ângulo inscrito $\small \mathrm{A\widehat{O}B}$ é dada por:

$\small \mathrm{Medida(A\widehat{O}B) = \frac{84^{\circ}}{2} = 42^{\circ}}$

Ângulo excêntrico interno

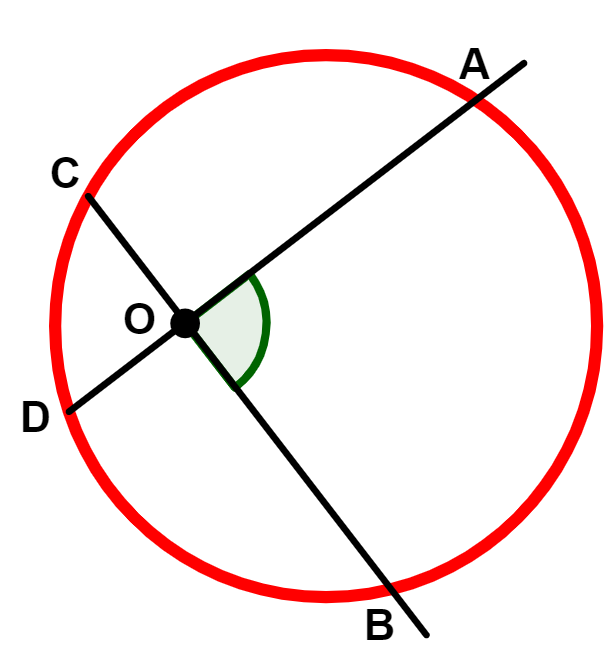
O ângulo cujo vértice está no interior da circunferência, mas não coincide com o centro, é chamado de ângulo excêntrico interno.

Na figura acima, o ângulo $\small \mathrm{A\widehat{O}B}$ é um ângulo excêntrico interno.

A medida desse ângulo excêntrico interno é dada por:

$\small \mathbf{Medida(A\widehat{O}B) = \frac{Medida \, de \, \widehat{AB}}{2} + \frac{Medida \, de \, \widehat{CD}}{2} }$

Ângulo excêntrico externo

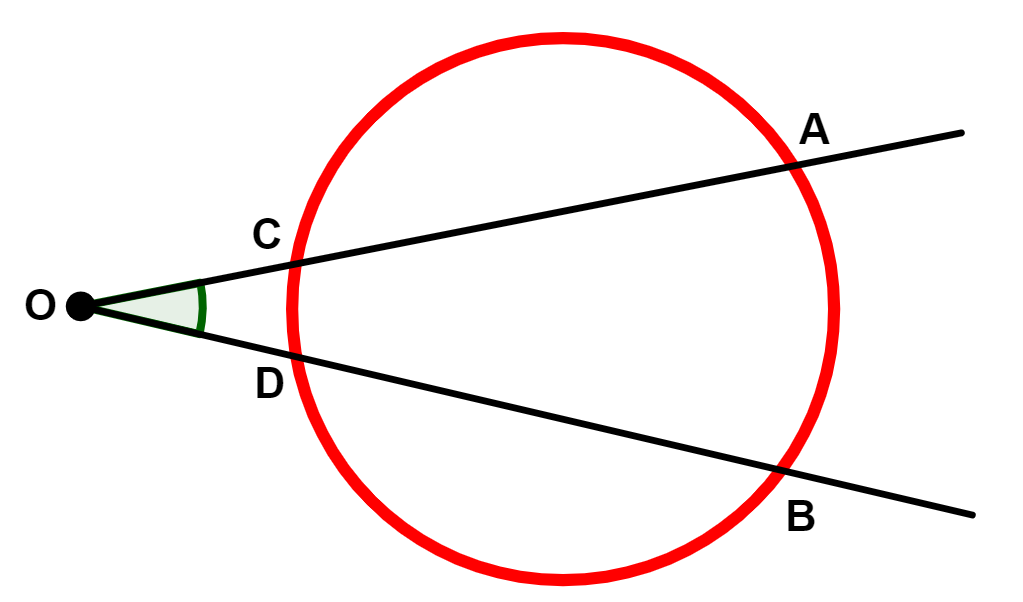
O ângulo cujo vértice está no exterior da circunferência, é chamado de ângulo excêntrico externo.

Na figura acima, o ângulo $\small \mathrm{A\widehat{O}B}$ é um ângulo excêntrico externo.

A medida desse ângulo excêntrico externo é dada por:

$\small \mathbf{Medida(A\widehat{O}B) = \frac{Medida \, de \, \widehat{AB}}{2} - \frac{Medida \, de \, \widehat{CD}}{2} }$

Você também pode se interessar:

Geometria plana