Condição de alinhamento de três pontos

Quando três pontos pertencem a uma mesma reta, eles são chamados de pontos alinhados.

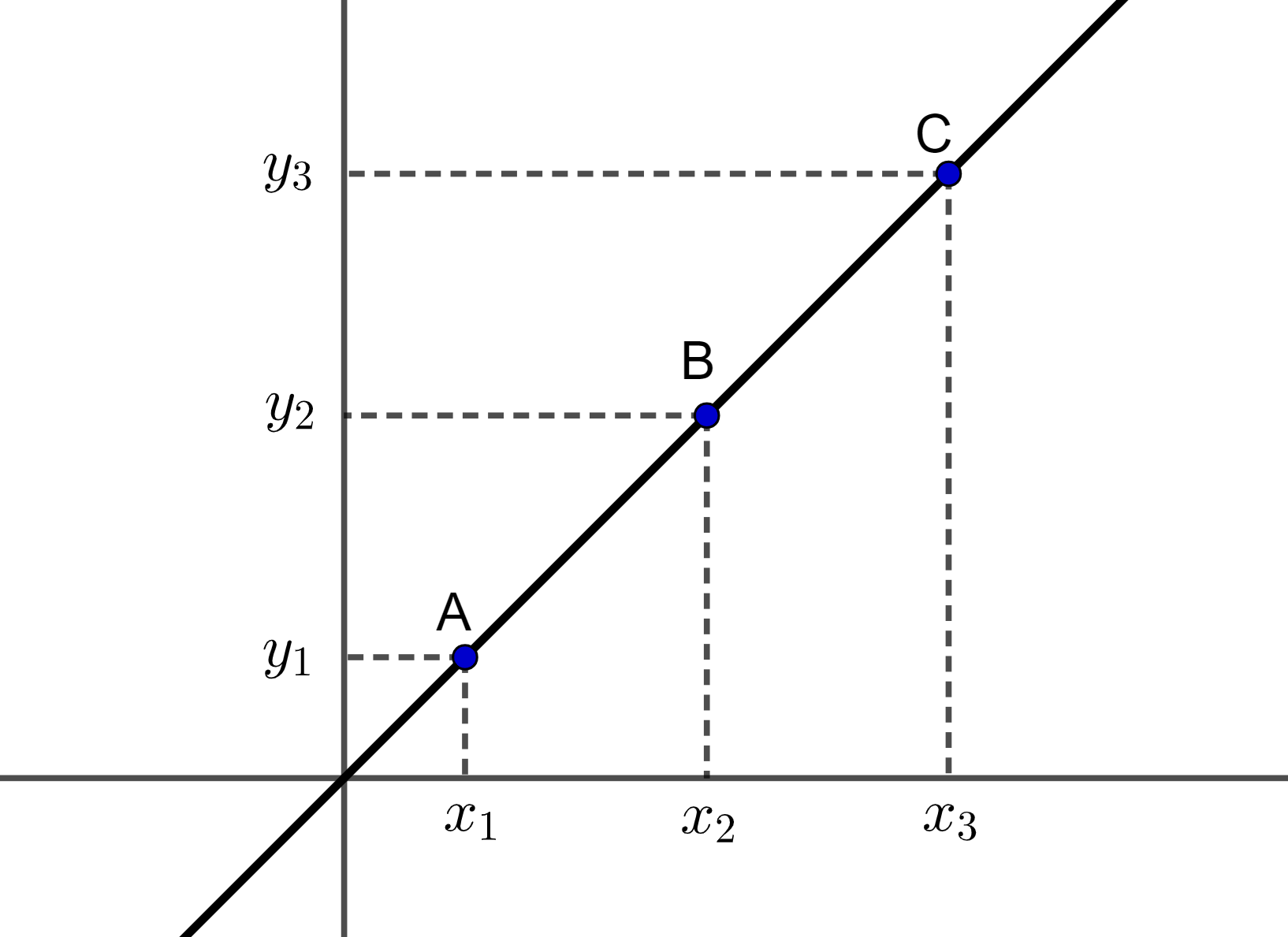
Na figura abaixo, os pontos ,  e  são pontos alinhados.

Condição de alinhamento de três pontos

Se os pontos A, B e C são alinhados, então, os triângulos ABD e BCE são triângulos semelhantes, logo, possuem lados proporcionais.

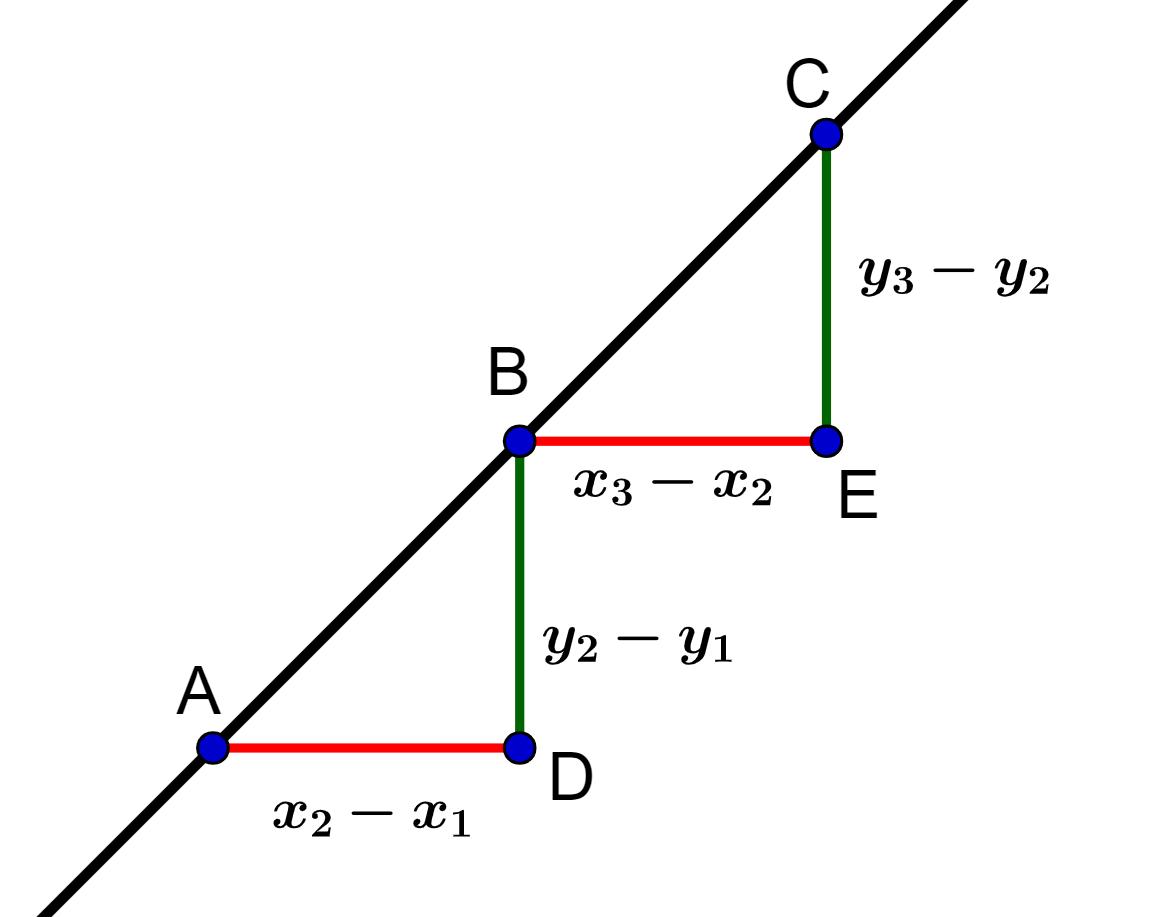
Assim, a condição de alinhamento de três pontos ,  e  quaisquer, é que seja satisfeita a seguinte igualdade:

Exemplos:

Verifique se os pontos estão alinhados:

a) (2, -1), (6, 1) e (8, 2)

Calculamos o primeiro lado da igualdade:

Calculamos o segundo lado da igualdade:

Como os resultados são iguais (2 = 2), então, os pontos estão alinhados.

b) (-2, 0), (4, 2) e (6, 3)

Calculamos o primeiro lado da igualdade:

Calculamos o segundo lado da igualdade:

Como os resultados são diferentes (3 ≠ 2), então, os pontos não estão alinhados.

Observação:

É possível mostrar que se: 

Então, o determinante da matriz de coordenadas dos pontos é zero, ou seja:

Portanto, outra forma de verificar se três pontos estão alinhados é a partir da resolução do determinante.

Você também pode se interessar:

• Equação da reta
• Retas perpendiculares
• Retas paralelas
• Como calcular a distância entre dois pontos
• Diferenças entre função e equação