Congruência de formas geométricas
Aprenda sobre congruência de formas geométricas: o que significa e como saber se duas figuras são ou não congruentes.
Na geometria, a palavra congruência está relacionada com a igualdade entre duas medidas.
Quando dois ângulos possuem a mesma medida, ou quando dois segmentos de reta são do mesmo tamanho, dizemos que são congruentes.
Entre formas geométricas, a congruência também está associada às medidas e não à forma ou posição das figuras.
Figuras geométricas congruentes
Vamos ver alguns exemplos de figuras congruentes para entender essa definição.
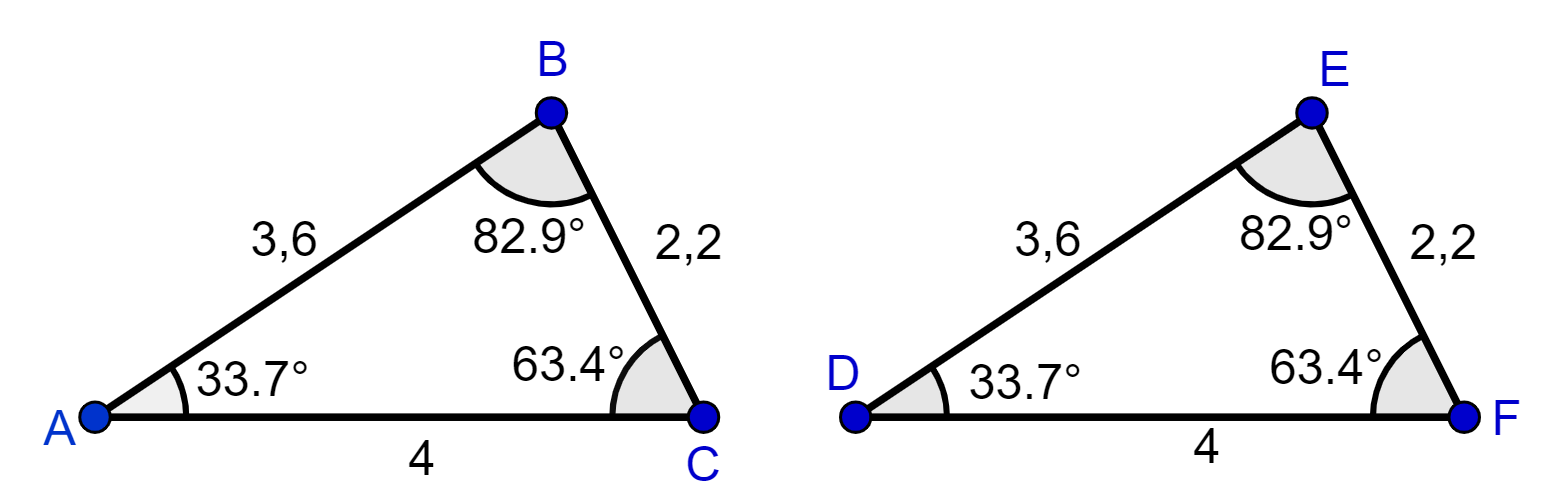
Os triângulos ABC e DEF, abaixo, são congruentes.
Observe que todos os lados correspondentes têm a mesma medida:
- AC e DF são lados correspondentes e ambos medem 4 unidades;
- AB e DE são lados correspondentes e ambos medem 3,6 unidades;
- BC e EF são lados correspondentes e ambos medem 2,2 unidades.
Em relação aos ângulos correspondentes, todos também têm a mesma medida:
- Os ângulos de vértices A e D são correspondentes e ambos medem 33,7°;
- Os ângulos de vértices C e F são correspondentes e ambos medem 63,4°;
- Os ângulos de vértices B e E são correspondentes e ambos medem 82,9°.
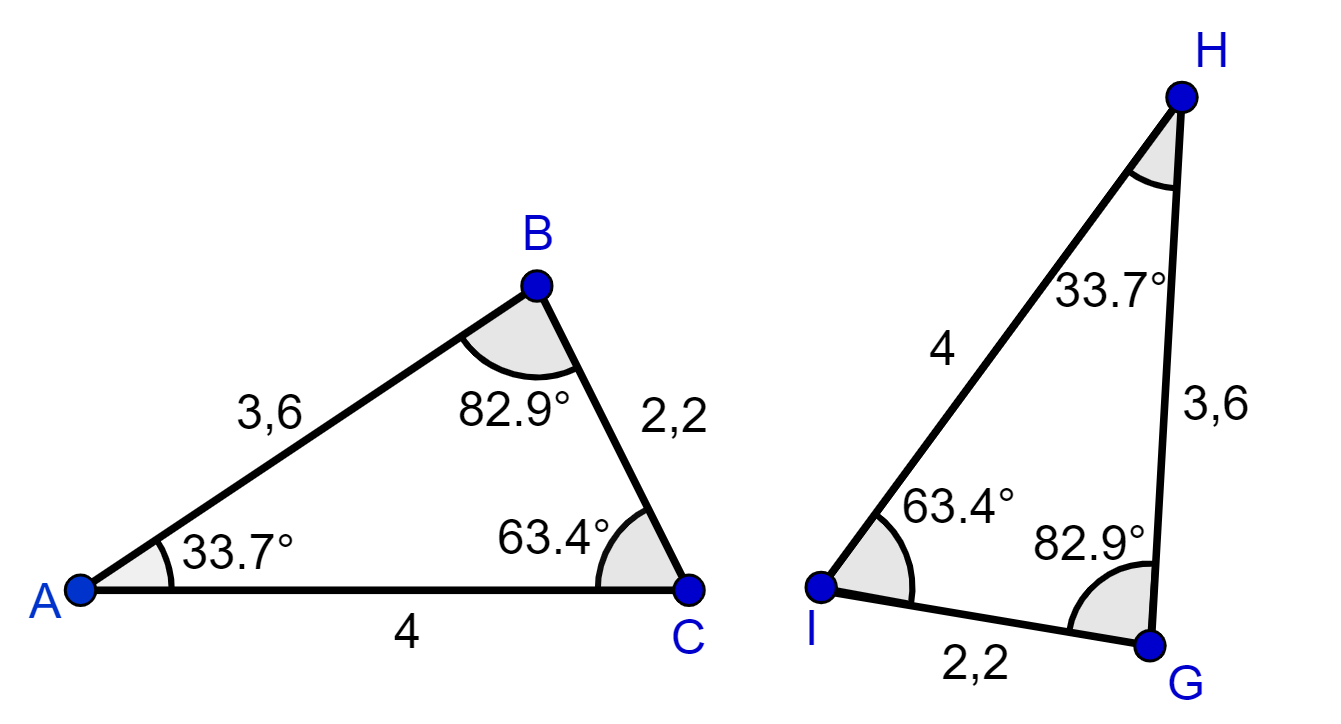
Os triângulos ABC e GHI, abaixo, também são congruentes.
Observe que, apesar da posição dos triângulos não ser a mesma, eles possuem lados e ângulos correspondentes de mesma medida, por isso, as figuras são congruentes.
Observando a posição dos triângulos acima, poderíamos até cometer o equívoco de dizer que eles não eram congruentes, simplesmente por não terem sido desenhados exatamente iguais.
Por isso, nada de ficar observando a posição da figura quando for verificar congruência!
Vamos ver mais um exemplo de figuras congruentes.
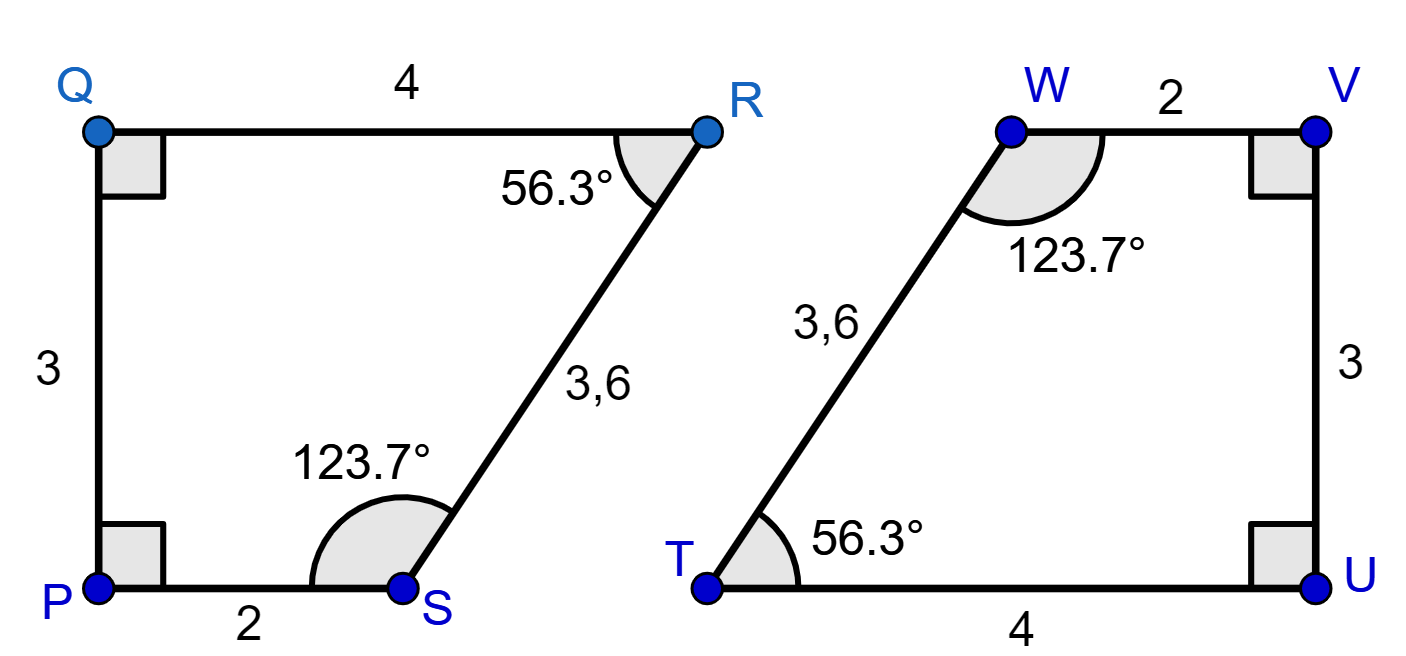
Os trapézios PQRS e TUVW possuem lados e ângulos correspondentes de mesma medida, portanto, são congruentes.
Você também pode se interessar:
- Congruência de triângulos
- Lista de exercícios sobre semelhança de triângulos
- Lista de exercícios sobre teorema de Tales

Os comentários estão fechados, mas trackbacks E pingbacks estão abertos.