Cônicas
Conheça as figuras geométricas cônicas: elipse, parábola e hipérbole. Entenda como elas são formadas, equação e características.
Cônicas ou seções cônicas são figuras geométricas de duas dimensões, que são obtidas quando um cone duplo de revolução é cortado por um plano.
As cônicas podem ser elipses, parábolas ou hipérboles. A circunferência é um caso específico de elipse.
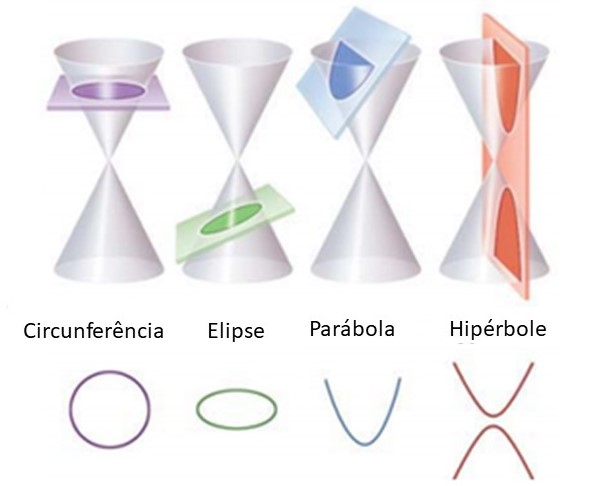
Elipse
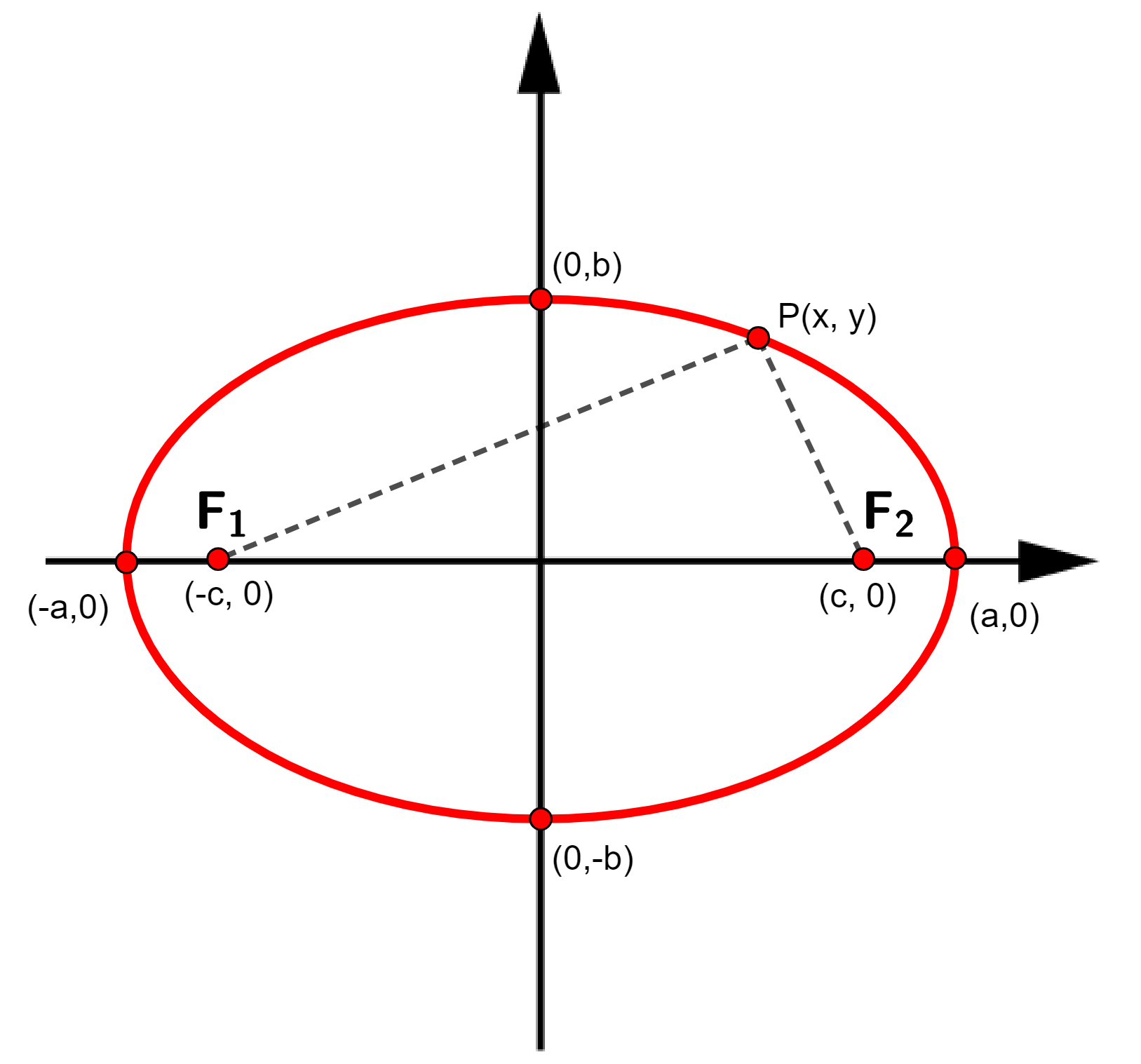
A elipse é definida como a figura geométrica formada por todos os pontos P(x, y) de um plano cuja distância de P até um ponto fixo somada a distância de P até outro ponto fixo
é sempre a mesma.
Elementos da elipse
- Centro: C(0,0);
- Vértices:
;
- Focos:
e
;
- Eixo maior:
(segmento que liga os vértices
);
- Eixo menor:
(segmento que liga os vértices
);
- Excentricidade:
(medida de achatamento da elipse).
A excentricidade da elipse é um valor entre 0 e 1, e quanto mais próximo de 0, mais a elipse se torna menos achatada e mais próxima de uma circunferência. Dessa forma, a circunferência é um caso particular de elipse, quando e = 0.
Equação reduzida da elipse
A equação reduzida ou equação canônica da elipse de focos e
é:
em que .
Parábola
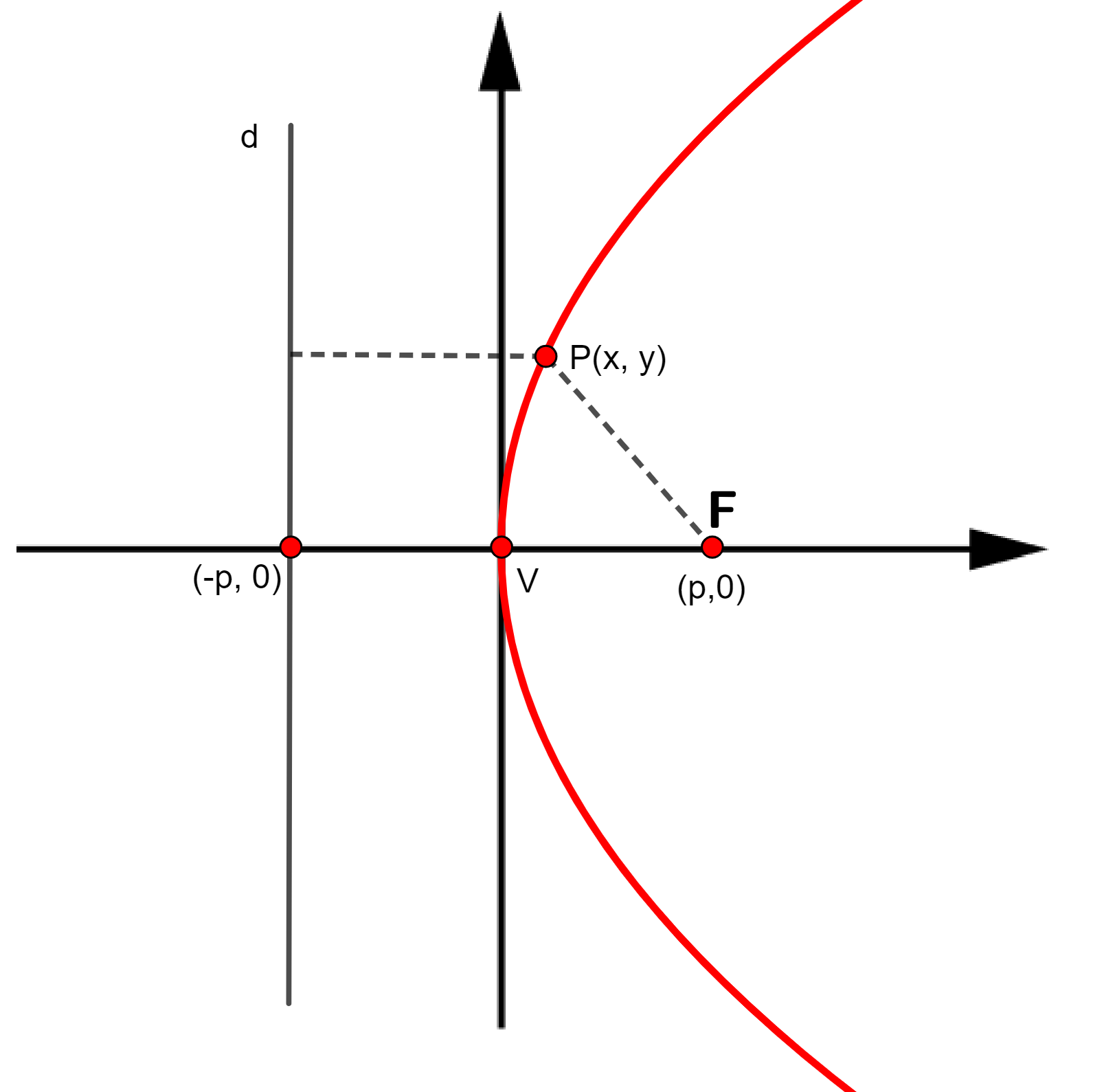
A parábola é definida como a figura geométrica formada por todos os pontos P(x, y) de um plano cuja distância de P até um ponto fixo F é igual à distância de P a uma reta fixa, que é chamada de diretriz.
Elementos da parábola
- Vértice: V(0,0);
- Foco: F(p, 0);
- Diretriz: reta d, com equação x = -p.
Equação reduzida da parábola
A equação reduzida ou equação canônica da parábola de foco e diretriz d correspondente a reta x = -p é:
De forma equivalente, a equação reduzida da parábola de foco e diretriz d correspondente a reta y = -p é:
A parábola y = x² é um caso particular quando p = 1/4.
Hipérbole
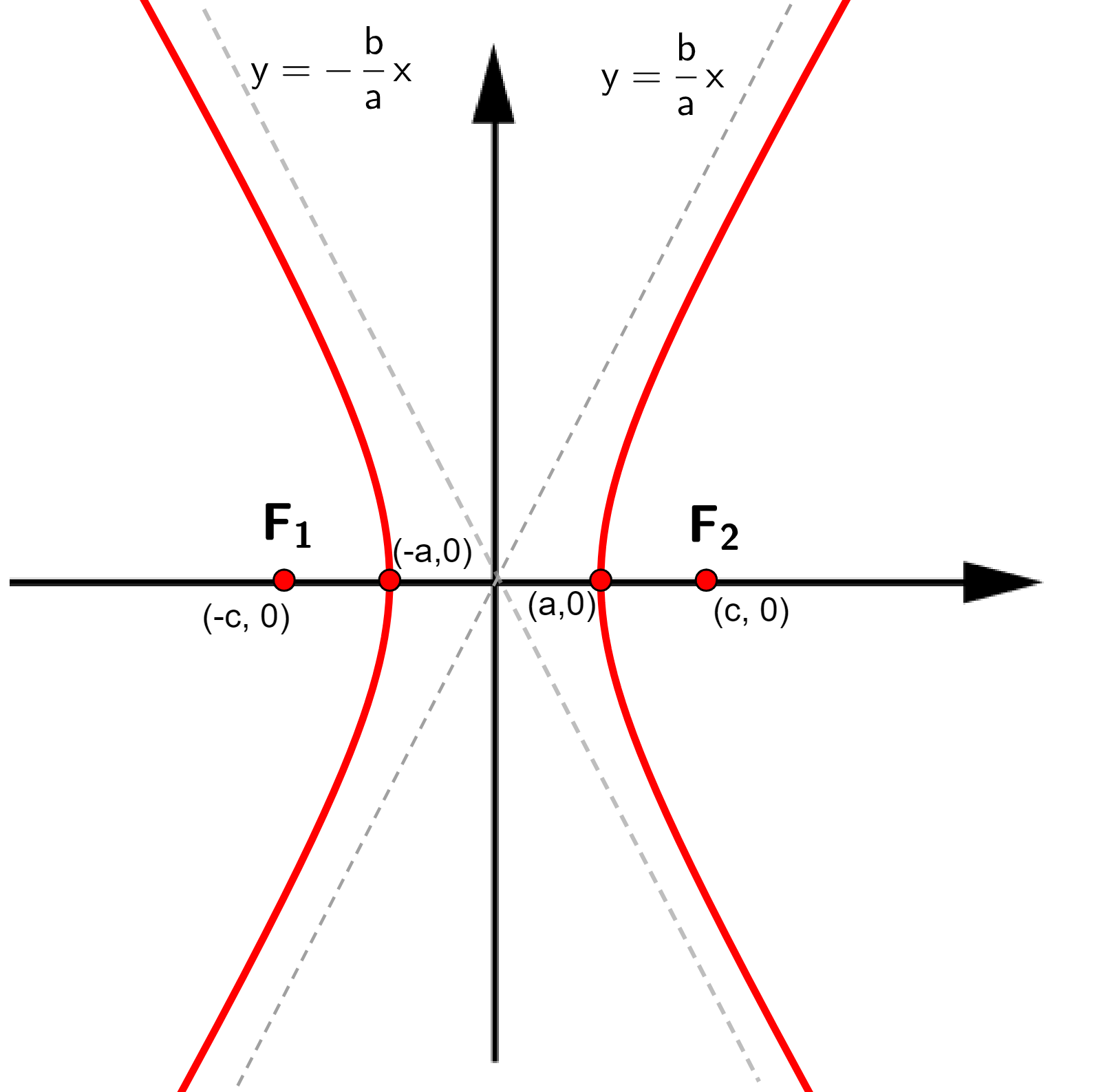
A hipérbole é definida como a figura geométrica formada por todos os pontos P(x, y) de um plano cujo módulo da diferença entre a distância de P até um ponto fixo e a distância de P até outro ponto fixo
é sempre o mesmo.
Elementos da hipérbole
- Centro: C(0,0);
- Vértices:
;
- Focos:
e
;
- Assíntotas:
e
;
- Excentricidade:
.
Equação reduzida da hipérbole
A equação reduzida ou equação canônica de uma hipérbole de focos e
é:
em que ou, de forma equivalente,
.
Você também pode se interessar:
- Áreas de figuras planas
- Teorema de Pitágoras – História, fórmula, Triângulo Pitagórico
- Como calcular a distância entre dois pontos
- Como fazer o gráfico da função do segundo grau

Os comentários estão fechados, mas trackbacks E pingbacks estão abertos.