Diagonais de um polígono
Saiba o que são as diagonais de um polígono e qual a fórmula para determinar o número de diagonais de um polígono.
Inicialmente, vamos lembrar que um polígono é uma figura geométrica plana formada por uma linha fechada que não possui curvatura, sendo determinada apenas por segmentos de reta.
Cada um dos segmentos de reta de um polígono é chamado de lados, os pontos de encontro entre os lados são chamados de vértices e cada ligamento entre um vértice e outro, passando pelo meio da figura é chamado de diagonal.
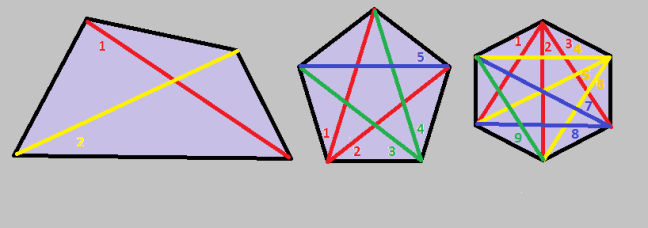
Devemos ressaltar que, para ser diagonal, os vértices não podem ser consecutivos, pois o ligamento entre vértices consecutivos determina um lado do polígono e não uma digonal.
Além disso, apesar do número de diagonais não coincidir com o número de lados do polígono, quanto mais lados a figura tem, mais diagonais ela vai ter também.
Desse modo, em polígonos com muitos lados torna-se difícil determinar o número de diagonais contando uma por uma. Felizmente, temos uma fórmula para facilitar esse cálculo.
Fórmula do número de diagonais de um polígono
A fórmula para determinar o número de diagonais de um polígono é dada por:
Onde:
D: número de diagonais;
n: número de lados do polígono.
Observe que para aplicar a fórmula tudo o que precisamos saber é o número de lados do polígono.
Exemplo: Quantas diagonais possui um dodecágono?
Um dodecágono tem 12 lados, ou seja, n = 12. Aplicando a fórmula:
Logo, o dodecágono possui 54 diagonais.
Veja mais alguns exemplos do número de diagonais D para outros polígonos. Sugestão: utilize a fórmula para chegar nesses valores.
Número de lados de um polígono a partir das diagonais
Para saber quantos lados tem um polígono dado o seu número de diagonais, devemos utilizar a fórmula de Bhaskara para encontrar as raízes da seguinte equação do 2° grau:
Onde:
n: número de lados
d: número de diagonais
Exemplo: Quantos lados tem um polígono com 104 diagonais?
Como d = 104, temos:
Calculando o discriminante:
Calculando o valor de n:
Obtemos e
.
Como o número de lados não pode ser um valor negativo, então, o número de lados desse polígono é 16.
Você também pode se interessar:

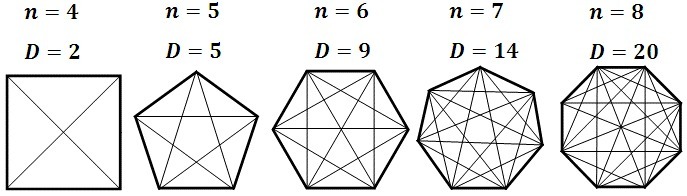
Os comentários estão fechados, mas trackbacks E pingbacks estão abertos.