Exercícios sobre equação da circunferência

Preparamos uma lista de exercícios resolvidos sobre a equação reduzida e geral de uma circunferência. Confira!

Por Elainy Marciano Publicado em 18/06/2020 - 16:55

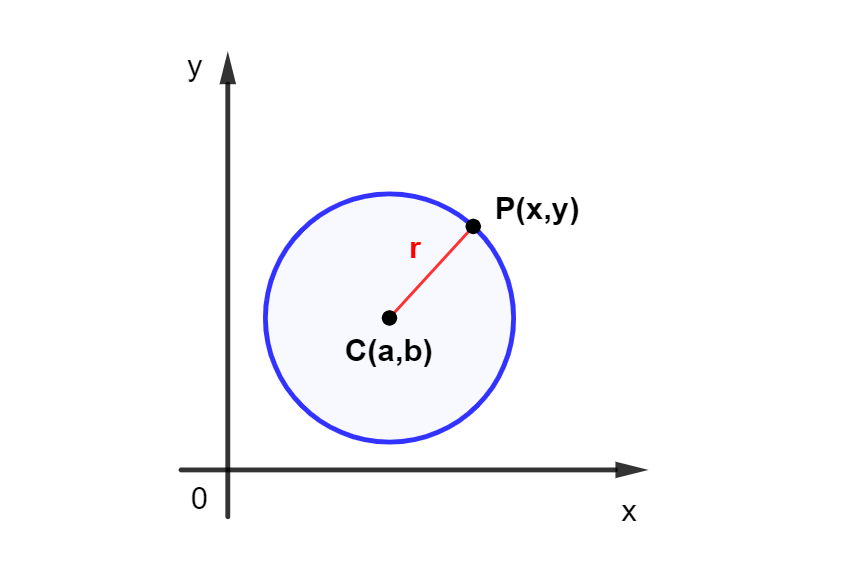
Em uma circunferência de centro C e raio r, a equação reduzida pode ser obtida calculando a distância entre o centro C e um ponto P da circunferência.

Veja mais

O limite numérico: até onde vai o maior número que conhecemos?

MEC suspende autorização de novos cursos à distância

Aplicando a fórmula da distância entre dois pontos, pode-se verificar que a equação reduzida da circunferência é dada por:

$\dpi{120} \mathrm{(x-a)^2 + (y-b)^2 = r^2}$

Desenvolvendo os quadrados da equação reduzida, encontramos a equação geral da circunferência:

$\dpi{120} \mathrm{x^2 +y^2 - 2ax - 2by + a^2 + b^2 - r^2 = 0}$

Para saber mais sobre esse assunto, confira uma lista de exercícios sobre a circunferência!

Lista de exercícios sobre a circunferência

Questão 1. Determine a equação reduzida e a equação geral de uma circunferência de centro (5, 3) e raio 2.

Questão 2. Os pontos (2, 3) e (-4, 1) pertencem à circunferência de centro (-2, 3) e raio 4?

Questão 3. Determine o centro e o raio de uma circunferência que possui a seguinte equação geral:

$\dpi{120} \mathrm{x^2 + y^2 - 2x + 4y -4 = 0}$

Questão 4. Determine o centro e o raio da circunferência que possui a seguinte equação geral:

$\dpi{120} \mathrm{x^2 + y^2 -4x + 2y = 0}$

Questão 5. Encontre a equação da circunferência de centro (3,1) e que passa pelo ponto (-3,4)

Questão 6. Encontre a equação da circunferência cujo centro é o ponto de interseção entre as retas x + 4y = 7 e 3x + y = -1 e o raio é igual a 3.

Resolução da questão 1

Temos centro (5, 3) e raio 2, ou seja, a = 5, b = 3 e r = 2.

Vamos substituir os valores de a, b e r para determinar a equação reduzida:

$\dpi{120} \mathrm{(x-a)^2 + (y-b)^2 = r^2}$

$\dpi{120} \Rightarrow \mathrm{(x-5)^2 + (y-3)^2 = 4}$

Para obter a equação geral, vamos desenvolver os quadrados:

$\dpi{120} \mathrm{x^2 - 10x + 25 + y^2 - 6y + 9 = 4}$

$\dpi{120} \Rightarrow \mathrm{x^2 + y^2 - 10x - 6y + 30 = 0}$

Resolução da questão 2

Para saber se os pontos pertencem ou não à circunferência, precisamos da sua equação.

Então, vamos verificar qual é a equação de uma circunferência de centro (-2, 3) e raio 4.

Temos a = -2, b = 3 e r = 4, assim, a equação reduzida é:

$\dpi{120} \mathrm{(x +2)^2 + (y-3)^2 = 16}$

Se um ponto (x, y) pertence a essa circunferência, ele deve satisfazer a sua equação, isto é, quando substituímos os valores de x e y no lado esquerdo da equação, o resultado deve ser igual a 16.

Vamos substituir cada um dos pontos dados em $\dpi{120} \mathrm{(x +2)^2 + (y-3)^2}$ .

Ponto (2,3) ⇒ x = 2 e y = 3

$\dpi{120} \mathrm{(x +2)^2 + (y-3)^2}$

$\dpi{120} =\mathrm{(2 +2)^2 + (3-3)^2}$

$\dpi{120} = 4^2 + 0^2$

$\dpi{120} = 16$

Como o resultado é igual a 16, então, o ponto (2,3) pertence à circunferência.

Ponto (-4,1) ⇒ x = -4 e y = 1

$\dpi{120} \mathrm{(x +2)^2 + (y-3)^2}$

$\dpi{120} =\mathrm{(-4 +2)^2 + (1-3)^2}$

$\dpi{120} =(-2)^2 + (-2)^2$

$\dpi{120} = 8$

Como o resultado é diferente de 16, então, o ponto (-4,1) não pertence à circunferência.

Resolução da questão 3

Com a equação reduzida, o centro e raio são facilmente determinados.

Então, vamos encontrar a equação reduzida dessa circunferência partindo de sua equação geral.

A equação geral é:

$\dpi{120} \mathrm{x^2 + y^2 - 2x + 4y -4 = 0}$

$\dpi{120} \Rightarrow \mathrm{x^2 - 2x + y^2 + 4y = 4}$

Vamos completar os trinômios quadrados perfeitos para obter os termos $\dpi{120} \mathrm{(x - a)^2}$ e $\dpi{120} \mathrm{(y - b)^2}$ da equação reduzida: $\dpi{120} \Rightarrow \mathrm{x^2 - 2x + 1^2 - 1^2 + y^2 + 4y + 2^2 - 2^2 = 4}$

$\dpi{120} \Rightarrow \mathrm{(x -1)^2 - 1^2 + (y+2)^2 - 2^2 = 4}$ $\dpi{120} \Rightarrow \mathrm{(x -1)^2 + (y+2)^2 = 4 + 1^2 + 2^2}$

$\dpi{120} \Rightarrow \mathrm{(x -1)^2 + (y+2)^2 = 9}$

$\dpi{120} \Rightarrow \mathrm{(x -1)^2 + (y+2)^2 = 3^2}$

Portanto, o centro é o ponto (1, -2) e o raio é 3.

Resolução da questão 4

Vamos determinar a equação reduzida, partindo da equação geral:

$\dpi{120} \mathrm{x^2 + y^2 -4x + 2y = 0}$

$\dpi{120} \Rightarrow \mathrm{x^2 -4x +y^2 +2y = 0}$

$\dpi{120} \Rightarrow \mathrm{x^2 -4x + 2^2 - 2^2 +y^2 +2y + 1^2 - 1^2 = 0}$

$\dpi{120} \Rightarrow \mathrm{(x - 2)^2 - 2^2 +(y + 1)^2 - 1^2 = 0}$

$\dpi{120} \Rightarrow \mathrm{(x - 2)^2 +(y + 1)^2 = 2^2 + 1^2}$

$\dpi{120} \Rightarrow \mathrm{(x - 2)^2 +(y + 1)^2 = 5}$

$\dpi{120} \Rightarrow \mathrm{(x - 2)^2 +(y + 1)^2 = (\sqrt{5})^2}$

Portanto, o centro é o ponto (2, -1) e o raio é √5.

Resolução da questão 5

Temos o centro da circunferência e falta o raio para determinarmos a equação da circunferência.

Devemos lembrar que o raio de uma circunferência é a distância entre o centro e qualquer ponto da circunferência.

Assim, sabendo que o centro é (3,1) e o ponto (-3,4) pertence à circunferência, o raio corresponde a distância entre os pontos (3,1) e (-3, 4).

Pela fórmula da distância entre dois pontos, temos que: $\dpi{120} r = \sqrt{(3 + 3)^2+(1 + 4)^2}$

$\dpi{120} r = \sqrt{36+25}$

$\dpi{120} r = \sqrt{61}$

Assim, a equação reduzida da circunferência é:

$\dpi{120} \mathrm{(x - 3)^2 + (y - 1)^2 = (\sqrt{61})^2}$

$\dpi{120} \Rightarrow \mathrm{(x - 3)^2 + (y - 1)^2 = 61}$

Resolução da questão 6

O ponto de intersecção entre as retas x + 4y = 7 e 3x + y = -1 corresponde a solução do sistema de equações:

$\dpi{120} \left\{\begin{matrix} \mathrm{x + 4y = 7}\\ \mathrm{3x + y = -1} \end{matrix}\right.$

x + 4y = 7 ⇒ x = 7 – 4y

Substituindo x por (7 – 4y) na segunda equação:

3x + y = -1 ⇒ 3. (7 – 4y) + y = -1 ⇒ 21 – 12y + y = -1

⇒ -11y = -1 – 21 ⇒ -11y = -22 ⇒ y = 22/11

⇒ y = 2

Então:

x = 7 – 4y ⇒ x = 7 – 4.2 ⇒ x = -1

Portanto, o ponto de intersecção é o ponto (-1, 2).

Sabendo que esse é o centro da circunferência e que o raio é 3, a equação da circunferência é:

$\dpi{120} \mathrm{(x + 1)^2+(y -2)^2 = 9}$

Você também pode se interessar: