Lista de exercícios de sequência numérica
Confira uma lista de exercícios resolvidos sobre sequências numéricas, termo geral, lei de formação, e muito mais!
As sequências numéricas são conjuntos de números que seguem uma ordem pré-estabelecida, ou seja, existe de um padrão entre eles.
A lei de formação ou termo geral de uma sequência é uma fórmula que define como os elementos da sequência são formados. A partir dela, podemos determinar qualquer termo de uma sequência.
No estudo das sequências numéricas, destacam-se as progressões aritméticas e progressões geométricas.
Ficou interessado nesse assunto e quer aprender mais?! Confira, a seguir, uma lista de exercícios de sequência numérica, todos com a resolução completa.
Exercícios de sequência numérica
Questão 1. Determine o próximo número da sequência:
19, 22, 25, 28, …
Questão 2. Determine o 5º número da sequência:
42, 38, 34, 30, …
Questão 3. Qual o número que continua a sequência?
12, 24, 48, 96, …
Questão 4. Qual o próximo número?
240, 120, 60, 30, …
Questão 5. Determine o valor de x na sequência:
6, 7, 9, 12, 16, 21, x
Questão 6. Qual o valor de x na sequência?
3, 6, 8, 16, 18, 36, x
Questão 7. Determine o valor de x na sequência:
5, 8, 7, 10, 9, 12, 11, x
Questão 8. Encontre o valor de x:
2, 7, 17, 32, 52, x
Questão 9. Determine o próximo número da sequência:
4, 9, 15, 23, 34, …
Questão 10. Determine o temo geral da sequência:
4, 9, 16, 25, 36, …
Questão 11. Determine o termo geral da sequência:
-4, 9, -16, 25, -36, …
Questão 12. Qual o termo geral da sequência?
5, 10, 17, 26, 37, …
Resolução da questão 1
Observe que cada número corresponde ao seu antecessor mais 3:
Portanto, o próximo número da sequência é 31, já que 28 + 3 = 31.
Resolução da questão 2
Observe que cada número corresponde ao seu antecessor menos 4:
Portanto, o próximo número é 26, já que 30 – 4 = 26.
Resolução da questão 3
Observe que cada número corresponde ao seu antecessor multiplicado por 2
Portanto, o próximo número é 192, já que 96 × 2 = 192.
Resolução da questão 4
Observe que cada número corresponde ao seu antecessor dividido por 2:
Portanto, o próximo número é 15, já que 30 : 2 = 15.
Resolução da questão 5
Observe que há um padrão:
Portanto, x = 21 + 6 = 27.
Resolução da questão 6
Observe que há um padrão, multiplica-se por 2 e soma-se 2, de forma alternada.
Portanto, x = 36 + 2 = 38.
Resolução da questão 7
Observe que há um padrão, soma-se 3 e subtrai-se 1, de forma alternada.
Portanto, x = 11 + 3 = 14.
Resolução da questão 8
Observe que há um padrão:
Portanto, x = 52 + 25 = 77.
Resolução da questão 9
Nesse caso, o padrão é observado em uma segunda etapa.
Para saber qual o próximo número da primeira fileira, devemos saber, antes, qual o próximo número da segunda fileira.
Pelo padrão observado, na terceira fileira, o próximo número da segunda fileira é 15, pois 11 + 4 = 15.
Então, o próximo número da primeira fileira é 34 + 15 = 49.
Resolução da questão 10
Queremos identificar o termo geral da sequência:
4, 9, 16, 25, 36, …
Observe que os termos são quadrados perfeitos. Então, podemos escrevê-la da seguinte forma:
2², 3², 4², 5², 6², …
Agora, considerando apenas a base de cada potência, veja que cada uma delas corresponde a posição que ocupa na sequência somado ao número 1.
Podemos reescrevê-la como:
(1+ 1)², (2 + 1)², (3 + 1)², (4 + 1)², (5 + 1)², …
Portanto, o termo geral é:
Resolução da questão 11
A diferença entre a sequência abaixo e a sequência do exercício anterior, é que nessa os termos de posição ímpar possuem sinal negativo.
-4, 9, -16, 25, -36, …
Podemos reescrevê-la como:
Portanto, o termo geral é:
Resolução da questão 12
Queremos encontrar o termo geral da sequência:
5, 10, 17, 26, 37, …
Observe que cada termos dessa sequência corresponde a um quadrado perfeito somado 1, isto é, 5 = 4 + 1, 10 = 9 + 1, 17 = 16 + 1, e assim por diante.
Então, podemos reescrevê-la como:
4 + 1, 9 + 1, 16 + 1, 25 + 1, 36 + 1, …
Considerando o termo geral da sequência (4, 9, 16, 25, 36, …), do exercício 10, o termo geral dessa outra sequência é:
Você também pode se interessar:
- Sequência de Fibonacci
- Plano de aula – Sequência numérica de 2 em 2
- Plano de aula – Sequência numérica de 5 em 5
- Lista de exercícios de progressão aritmética
- Lista de exercícios de progressão geométrica

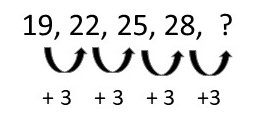
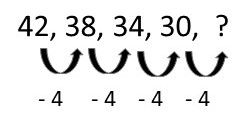
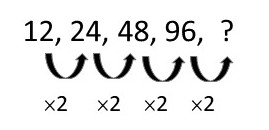
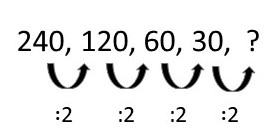
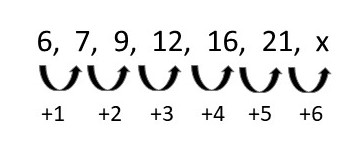
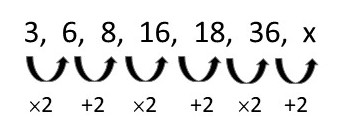


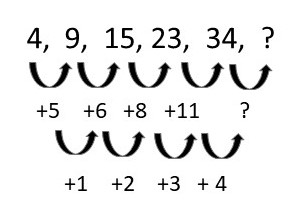
Os comentários estão fechados, mas trackbacks E pingbacks estão abertos.