Fórmula de Bhaskara
Confira agora as etapas para realizar a fórmula de Bhaskara. Além disso, confira exemplo do desenvolvimento da equação matemática.
A fórmula de Bhaskara é um cálculo matemático criado pelo professor e astrólogo indiano Bhaskara Akaria. A função da fórmula é determinar as raízes de uma função de segundo grau. Esse objetivo é alcançado pelos coeficientes.
Logo, para resolver a equação da fórmula de Bhaskara, é necessário substituir os valores dos coeficientes e, assim, realizar os cálculos formados. Para isso, é importante entender que uma legítima equação de segundo grau foi formada.
Mas, como saber que uma equação de segundo grau foi formada? É simples, basta atender à seguinte estrutura: ax² + bx + c = 0. Os números correspondentes às letras a, b e c devem ser naturais e a não pode ser igual a zero. Além disso, b deve ser multiplicado por x, enquanto c não multiplica pela incógnita.
Fórmula de Bhaskara
Confira abaixo a fórmula de Bhaskara:
Confira as etapas para realizar a fórmula de Bhaskara:
Esse é o primeiro passo a ser dado para resolver uma equação de segundo grau. Como dito anteriormente, para saber se a fórmula está correta, é necessário entender se uma equação de segundo grau legítima foi formada.
Vale lembrar que existem três pontos a considerar:
- ∆ > 0 → Duas raízes reais e distintas;
- ∆ =0 → Duas raízes reais e iguais;
- ∆ <0 → Sem raízes na equação.
2. Bhaskara
Após encontrar o valor de ∆ (delta), é necessário passar para a segunda etapa, que é substituir os coeficientes na fórmula. Confira abaixo:
3. Resultado (raízes)
Essa é a última etapa do processo, onde os resultados são encontrados. Enquanto XI segue o discriminante positivo, o XII segue o discriminante negativo. Confira abaixo:
Fórmula de Bhaskara: exemplo
No exemplo abaixo, vamos considerar que a = 1, b = -2 e c = 1.
1. Na primeira etapa, conhecida como discriminante, os coeficientes serão aplicados à fórmula para encontrar o resultado de ∆ (delta):
2. Na segunda etapa, após encontrar o ∆ (delta), será necessário substituir na fórmula:
3. Por fim, encontra-se o resultado das raízes:
Leia também:
- Problemas de matemática – Atividades Educativas para imprimir
- Quadrados mágicos – Origem, definição e dicas de como resolver
- Charadas matemáticas com respostas

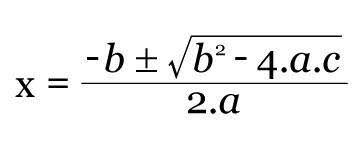
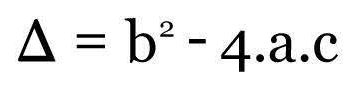
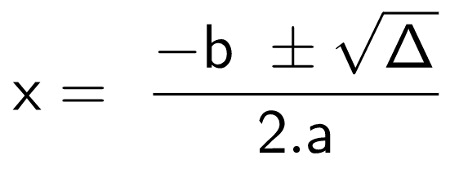

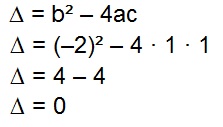
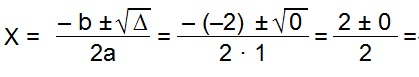
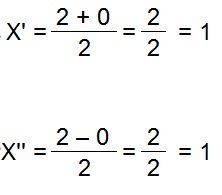
Os comentários estão fechados, mas trackbacks E pingbacks estão abertos.