Função do primeiro grau (função afim)
Saiba o que é uma função do primeiro grau ou função afim, aprenda a construir o gráfico e a determinar se a função é crescente ou decrescente.
Uma função do primeiro grau, ou função afim, é qualquer função que pode ser descrita da seguinte forma:
Onde a e b são números reais quaisquer.
A variável x é chamada de variável independente, e o conjunto de números que essa variável assume é chamado de domínio da função. Enquanto isso, y = f(x) é chamada de variável dependente, e o conjunto de números que y assume é chamado de contradomínio.
Exemplos de funções do primeiro grau:
a) 2x + 1 → a = 2 e b = 1
b) -x + √9 → a = -1 e b = √9
c) 5x → a = 5 e b = 0
Observe que em todas essas funções o expoente da variável independente é 1, ou seja, x¹ = x. Funções com o expoente diferente de 1, como x² – 3, não são funções do primeiro grau.
Gráfico de uma função do primeiro grau
O gráfico de uma função do primeiro grau é sempre uma reta, o que irá mudar de uma função para outra é a inclinação e a localização da reta no plano cartesiano, que dependerá dos valores de a e de b.
Lembre-se que por dois pontos passam uma única reta, então, para construir o gráfico de uma função do primeiro grau, basta encontrar dois pares ordenados que pertencem a essa reta.
Para encontrar esses dois pares ordenados, basta escolher dois valores para x e substituir na função para encontrar os valores de y.
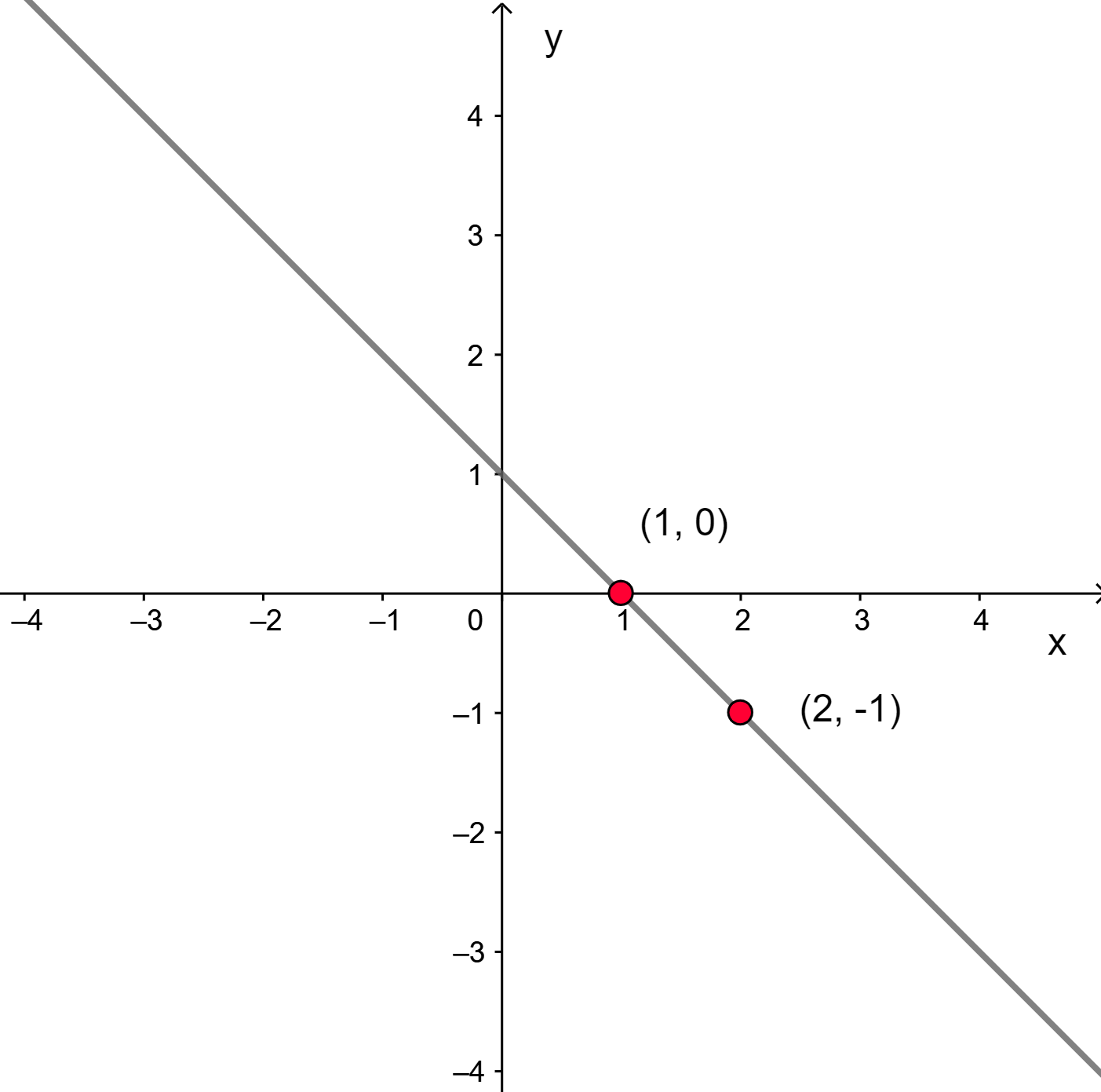
Exemplo: Construir o gráfico da função f(x) = – x + 1.
Para x = 1, temos f(1) = -1 + 1 = 0, então, temos o par ordenado (1, 0).
Para x = 2, temos f(2) = -2 + 1 = -1, então, temos o par ordenado (2, -1).
Agora, construímos o plano cartesiano e marcamos esses dois pontos, traçando uma reta que passa por eles:
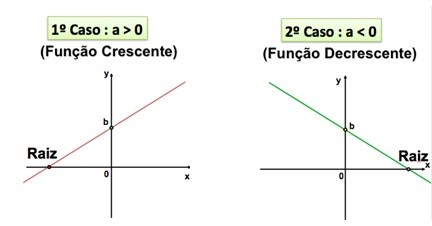
Função crescente e função decrescente
A função do primeiro grau pode ser uma função crescente ou uma função decrescente, isso dependerá do valor de a.
- Se a é um valor positivo (a > 0), a função é crescente.
- Se a é um valor negativo (a < 0), a função é decrescente.
Em uma função crescente, a medida que o valor de x aumenta, o valor de y também aumenta. Já em uma função decrescente, quando x aumenta, y diminui, ou vice-versa.
Como a inclinação da reta depende do valor de a, esse valor também é chamado de coeficiente angular. Já o valor de b, é o valor onde a reta cruza o eixo y, por isso, ele é chamado de coeficiente linear.
Então, em uma função f(x) = ax + b, temos que:
- a: é o coeficiente angular.
- b: é o coeficiente linear.
Outra observação é que o valor onde a reta cruza o eixo x é chamado de raiz ou zero da função do primeiro grau.
Raiz da função do primeiro grau
A raiz ou zero de uma função do primeiro grau é o valor que x assume quando y é igual a zero. Assim, para determinar a raiz de uma função, basta igualar a função ao valor 0 e encontrar o valor de x.
Exemplos: Encontrar a raiz das funções abaixo.
a) f(x) = 2x – 6
2x – 6 = 0
2x = 6
x = 6/2
x = 3
Então, a raiz dessa função é 3.
b)f(x) = -x + 0,5
-x + 0,5 = 0
-x = -0,5
x = 0,5
Logo, a raiz dessa função é 0,5.
Você também pode se interessar:

Os comentários estão fechados, mas trackbacks E pingbacks estão abertos.