Exercícios de função do primeiro grau (função afim)

Veja uma lista de exercícios resolvidos sobre funções do primeiro grau, também conhecidas como função afim.

Por Elainy Marciano Publicado em 30/04/2020 - 16:13

As funções do primeiro grau também são conhecidas como função afim e são expressas da seguinte forma:

f(x) = ax + b

Veja mais

O limite numérico: até onde vai o maior número que conhecemos?

Reditec debate ensino profissional e tecnológico

x é a variável independente;
y = f(x) é a variável dependente;
a é um número real, chamado de coeficiente angular;
b é um número real, chamado de coeficiente linear.

O gráfico dessa função é uma reta com inclinação determinada pelo valor do coeficiente angular a e que cruza o eixo y no ponto b, ou seja, no coeficiente linear.

A seguir, temos uma lista de exercícios resolvidos sobre função do primeiro grau, para você praticar e tirar suas dúvidas sobre o assunto.

Exercícios de função do primeiro grau (função afim)

Questão 1. O gráfico da função f(x) = 3x + 5 não passa por um dos quadrantes do plano cartesiano. Esse quadrante é:

a) I

b) II

c) IV

d) III

Questão 2. Determine o valor do coeficiente angular de cada uma das retas abaixo:

a) y = 2 – 3x

b) y = 2.(3x – 4)

c) y = (2x + 1) / 2

d) 3x + 4y = 1

Questão 3. Encontre a equação da reta que passa pelos seguintes pontos:

a) A(2, -1) e B(5, 2)

b) C(0, 6) e D(1, 11)

Questão 4. Considerando uma função do primeiro grau f(x) = ax +b, tal que f(0) = 7 e f(1) = 11, determine o valor de a – b.

Questão 5. Qual é a função afim definida por uma reta que cruza o eixo x no ponto 4 e o eixo y no ponto 3?

a) f(x) = 5x

b) f(x) = -3x + 4

c) f(x) = 3/4x + 3

d) f(x) = – 3/4x + 3

Questão 6. Se f(x) é uma função do primeiro grau com coeficiente angular igual a 8 e ponto de intercepto ao eixo y igual a 5, determine o valor de f(-1) + f(0) + f(1).

Questão 7. (UFPI) A função real com variável real, dada por f(x) = (3 – 2a)x + 2, é crescente quando:

a) a > 0

b) a < 3/2

c) a = 3/2

d) a > 3/2

e) NDA

Questão 8. (U. E. Londrina) Seja a função f, tal que f(x) = ax + b. Se os pontos (0, -3) e (2, 0) pertencem ao gráfico de f, então a + b é igual a:

a) 9/2

b) 3

c) 3/2

d) -3/2

e) 1

Resolução da questão 1

Existem algumas formas de resolver essa questão:

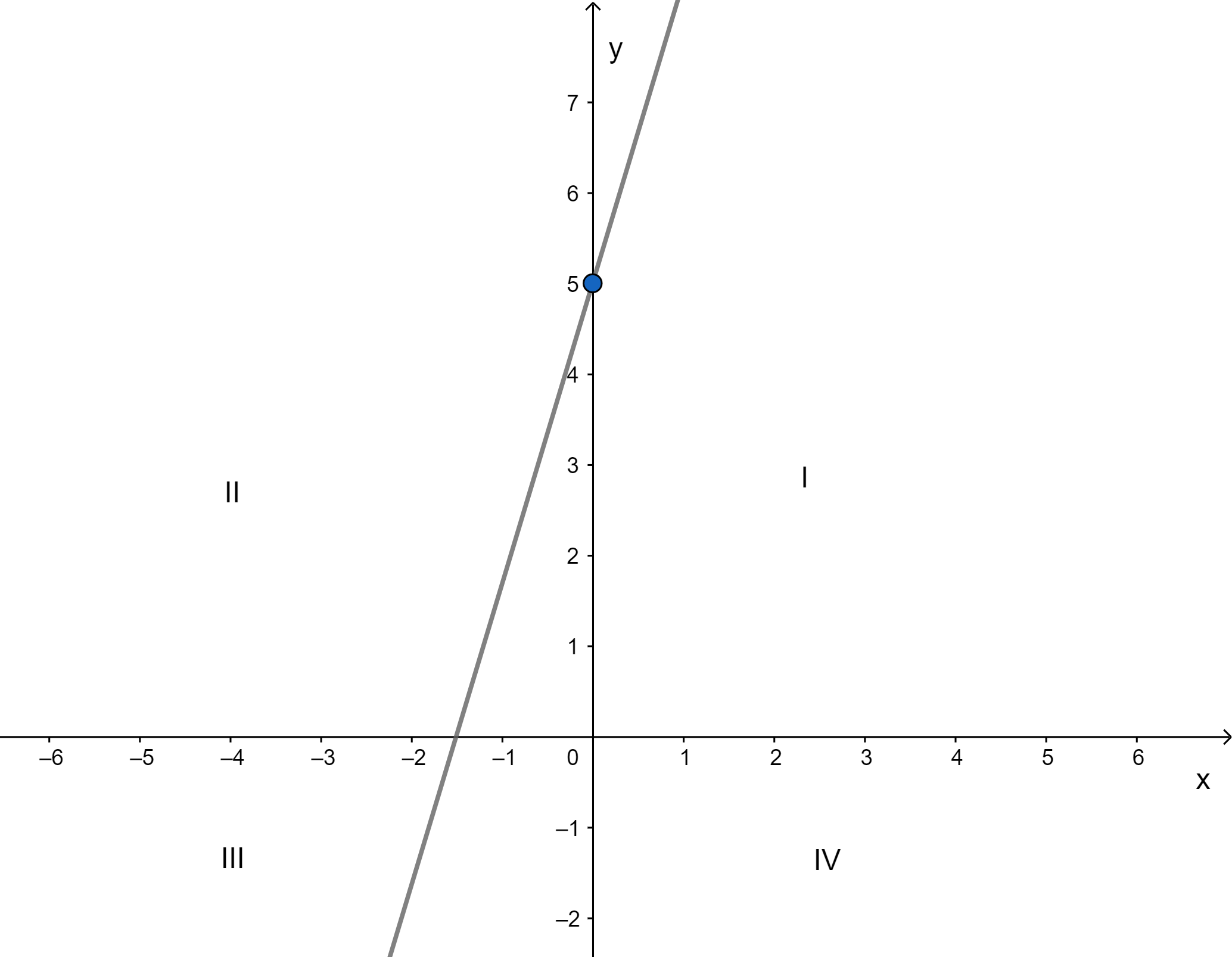
Podemos determinar dois pares ordenados pelos quais passa a reta da equação e, em seguida, traçamos a reta para verificar sobre qual quadrante ela não passa.

Assim como também podemos observar que:

a = 3 → então é uma função crescente;

b = 5 → então a reta cruza o eixo y nesse ponto.

Então, fazendo um simples esboço do gráfico, notamos que ela não passa pelo quadrante IV.

Logo, a alternativa correta é a letra c.

Resolução da questão 2

Para determinar o coeficiente angular, a equação deve estar expressa da seguinte forma:

y = ax + b

A constante a que multiplica a variável x é o coeficiente angular.

a) y = 2 – 3x ⇒ y = – 3x + 2

Logo, temos a = -3.

b) y = 2.(3x – 4) ⇒ y = 6x – 8

Então, a = 6.

c) y = (2x + 1) / 2 ⇒ y = x + ½

Assim, a = 1.

d) 3x + 4y = 1 ⇒ 4y = 1 – 3x ⇒ y = (1 – 3x)/4 ⇒ y = 1/4 – 3x/4 ⇒ y = (-3/4).x + 1/4

Logo, a = -3/4.

Resolução da questão 3

a) A(2, -1) e B(5, 2)

Dados dois pontos da reta, podemos determinar o valor do coeficiente angular:

a = -1 – 2 / 2 – 5

a = -3 / -3

a = 1

Agora, encontramos a equação da reta a partir do coeficiente angular e um dos pontos dados:

Usando a = 1 e o ponto A(2,-1), temos que:

y – (-1) = 1.(x -2)

y + 1 = x – 2

y = x – 2 -1

y = x – 3 → essa é a equação da reta.

b) C(0, 6) e D(1, 11)

a = 6 – 11 / 0 – 1

a = -5 / -1

a = 5

Considerando o valor do coeficiente angular e o ponto C(0, 6), temos que:

y – 6 = 5 (x – 0)

y – 6 = 5x

y = 5x + 6

Resolução da questão 4

Temos que f(0) = 7 e f(1) = 11, ou seja, a reta passa pelos pontos (0, 7) e (1, 11), assim:

a = 7 – 11 / 0 – 1

a = -4 / -1

a = 4

Considerando a = 4 e o ponto (1 , 11), temos que:

y – 11 = 4.(x – 1)

y – 11 = 4x – 4

y = 4x – 4 + 11

y = 4x + 7 → equação da reta

Logo, b = 7 e a – b = 4 – 7 = -3.

Resolução da questão 5

Se a reta cruza o eixo y no ponto 3, então o valor do coeficiente linear b é 3.

Agora, precisamos determinar o valor do coeficiente angular, a.

Considerando que a reta passa pelos pontos (0, 3) e (4, 0), temos que:

a = 3 – 0 / 0 – 4

a = 3 / -4

a = -3/4

Assim, f(x) = -3/4x + 3. A alternativa correta é a letra d.

Resolução da questão 6

Considerando f(x) = ax + b, temos que a = 8 e b = 5. Então:

f(x) = 8x + 5

Assim:

f(-1) = 8. (-1) + 5 = -8 + 5 = -3

f(0) = 8.0 + 5 = 5

f(1) = 8.1 + 5 = 8 + 5 = 13

Logo, f(-1) + f(0) + f(1) = -3 + 5 + 13 = 15.

Resolução da questão 7

Para que f(x) = (3 – 2a)x + 2 seja uma função crescente, a constante que multiplica a variável x deve ser positiva, ou seja,

3 – 2a > 0

Vamos resolver essa inequação para determinar o valor de a:

3 – 2a > 0

-2a > -3

2a < 3

a < 3/2

Logo, a alternativa correta é a letra b.

Resolução da questão 8

Considerando os pontos (0, -3) e (2, 0), vamos determinar o valor de a:

a = -3 – 0/0 -2

a = -3 / -2

a = 3/2

A partir de a = 3/2 e o ponto (0, -3), vamos encontrar a equação da reta:

y – (-3) = 3/2(x – 0)

y + 3 = 3/2x

y = 3/2x – 3 → equação da reta

Assim, b = -3. Agora podemos calcular a + b

a + b = 3/2 -3 = (3 – 6)/2 = -3/2

Portanto, a alternativa correta é a letra d.

Você também pode se interessar: