Função injetora
Entenda o que é uma função injetora, veja exemplos e saiba como é o gráfico desse tipo de função.
Você sabe o que é função injetora? Uma função é injetora quando os diferentes elementos do domínio da função resultam em elementos diferentes do contradomínio, ou seja, nenhum elemento tem a mesma imagem que outro.
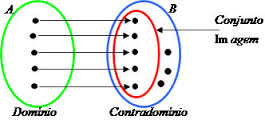
Recorde o que é domínio, contradomínio e imagem de uma função, através do diagrama abaixo.
Sendo f: A → B, temos:
Exemplos:
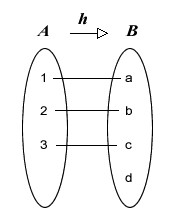
a) A função h: A → B é injetora.
Observe que cada elemento do domínio está ligado a um elemento diferente do contradomínio:
h(1) = a, h(2) = b e h(3) = c.
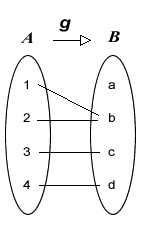
b) A função g: A → B não é injetora.
Observe que g(1) = b e g(2) = b, ou seja, os elementos 1 e 2 do domínio possuem a mesma imagem, b. Isso torna essa função não injetora.
Gráfico de uma função injetora
Vamos ver os gráficos de uma função injetora e de uma função não injetora para observar as diferenças.
Veja que cada valor de y está associado a apenas um valor de x.
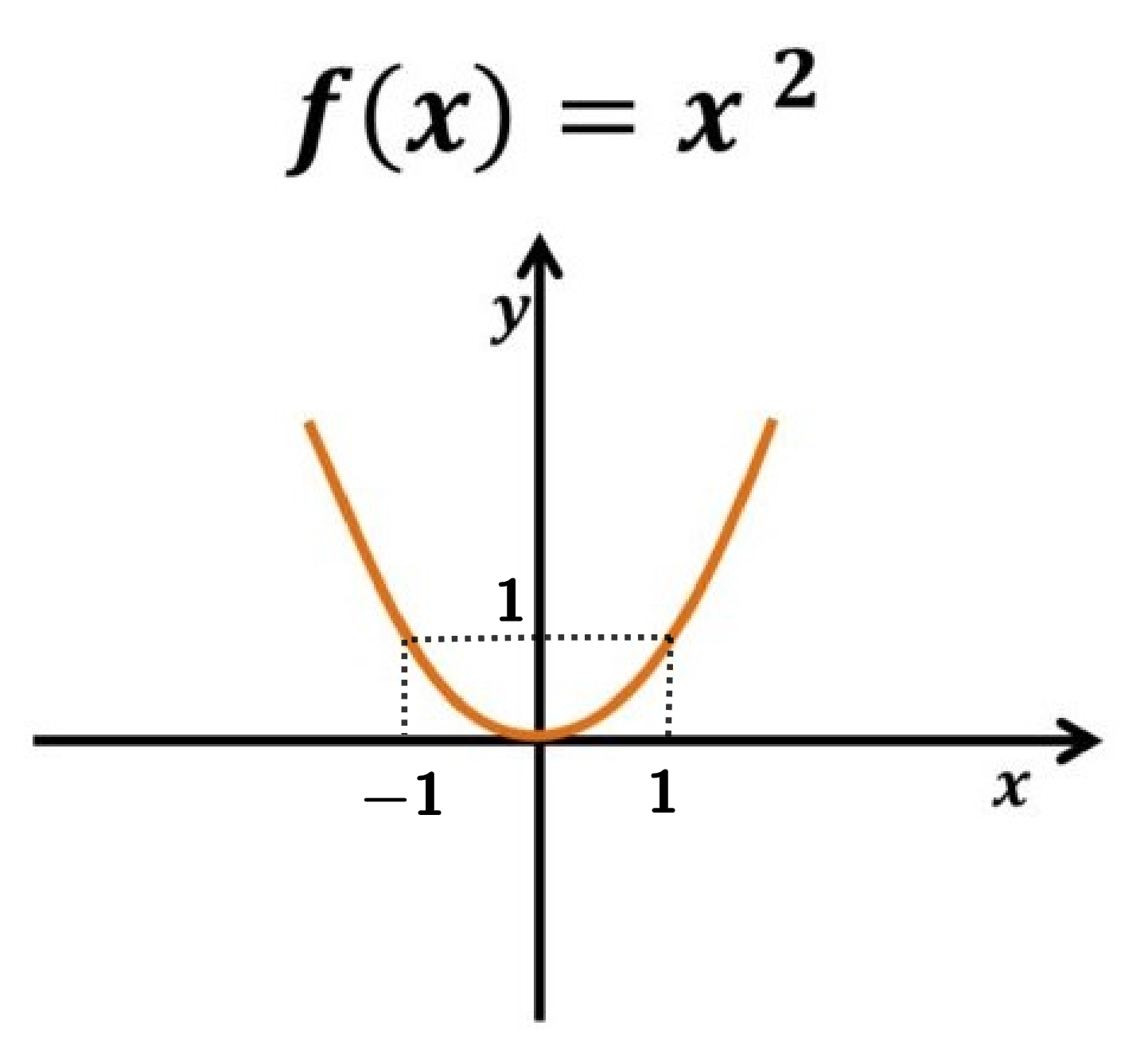
Observe que f(1) = 1 e f(-1) = 1 também, ou seja, o valor y =1 é imagem de dois pontos diferentes do domínio.
Você também pode se interessar:
- Função do primeiro grau (função afim)
- Exercícios de função do primeiro grau (função afim)
- Funções trigonométricas – Seno, cosseno e tangente

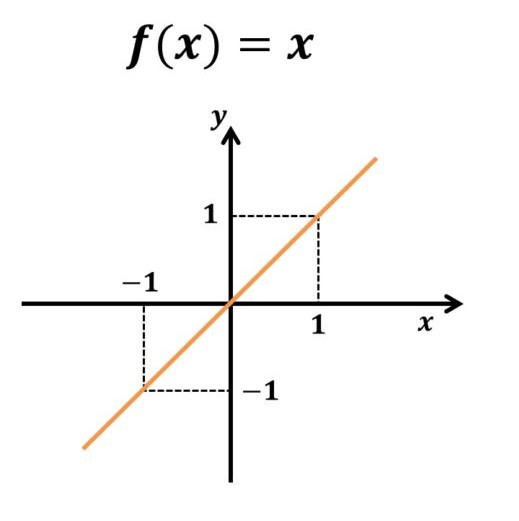
Os comentários estão fechados, mas trackbacks E pingbacks estão abertos.