Função modular

Definição, exemplos, domínio, imagem e construção do gráfico, aprenda tudo isso e muito mais sobre a função modular!

Por Elainy Marciano Publicado em 06/08/2020 - 22:08

A função modular é uma função que apresenta uma expressão algébrica dentro do módulo. Assim, são exemplos de função modular:

Veja mais

O limite numérico: até onde vai o maior número que conhecemos?

Reditec debate ensino profissional e tecnológico

O que é módulo?

Para compreender bem uma função modular, devemos lembrar que o módulo de um número corresponde a distância do número até o 0 na reta numérica, e que distâncias são sempre maiores ou iguais a zero, nunca negativas.

Dessa forma, quando temos incógnitas dentro do módulo, há três opções:

$|x| = \left\{\begin{matrix}\: \: \: \: \: x, \: se \: x> 0\\ \: \: \: \: 0, \: se \: x = 0 \\ - x,\: se \: x< 0 \end{matrix}\right.$

Exemplo:

se , então,
se , então,
se , então,

Isso acontece porque a distância de 0 a 7 é a mesma distância de -7 a 0, ambas são iguais a 7 unidades e a distância de 0 até 0 é 0 mesmo, não há deslocamento.

Domínio e imagem da função modular

Uma função modular pode ser definida como $f:\mathbb{R}\rightarrow \mathbb{R}$ , em que:

$f(x)=|x| = \left\{\begin{matrix}\: \: \: \: \: x, \: se \: x> 0\\ \: \: \: \: 0, \: se \: x = 0 \\ - x,\: se \: x< 0 \end{matrix}\right.$

O domínio da função modular é o conjunto dos números reais, já a imagem é o conjunto dos números reais não negativos.

$D(f) = \mathbb{R}$

$Im(f) = \mathbb{R}_+$

Isso significa que para qualquer valor de x, o valor calculado de f(x) será um valor maior ou igual a zero. Se x for zero ou um número positivo, f(x) é o próprio x. Mas se x for negativo, f(x) é o valor de x multiplicado por -1, para que o resultado seja positivo.

Exemplo:

$f(x) = |x-2| = \left\{\begin{matrix} \: \: \: \: (x - 2), \: se\: x -2 >0\\ \: \: \: \: \: \: \: 0, {\color{White} 1111} se\: x-2 =0 \\ -(x-2), \: se\: x - 2< 0 \end{matrix}\right.$

Como:

$x - 2> 0\Rightarrow x> 2$

$x - 2 = 0\Rightarrow x = 2$

$x - 2< 0 \Rightarrow x <2$ Podemos reescrever f(x) da seguinte forma:

$f(x) = |x-2| = \left\{\begin{matrix} \: \: \: \: (x - 2), \: se\: x >2\\ \: \: \: \: \: \: \:0 , {\color{White} 1111} se\: x =2 \\ -(x-2), \: se\: x <2 \end{matrix}\right.$

Gráfico da função modular

O gráfico de uma função que está dentro de um módulo fica sempre na parte positiva do eixo y.

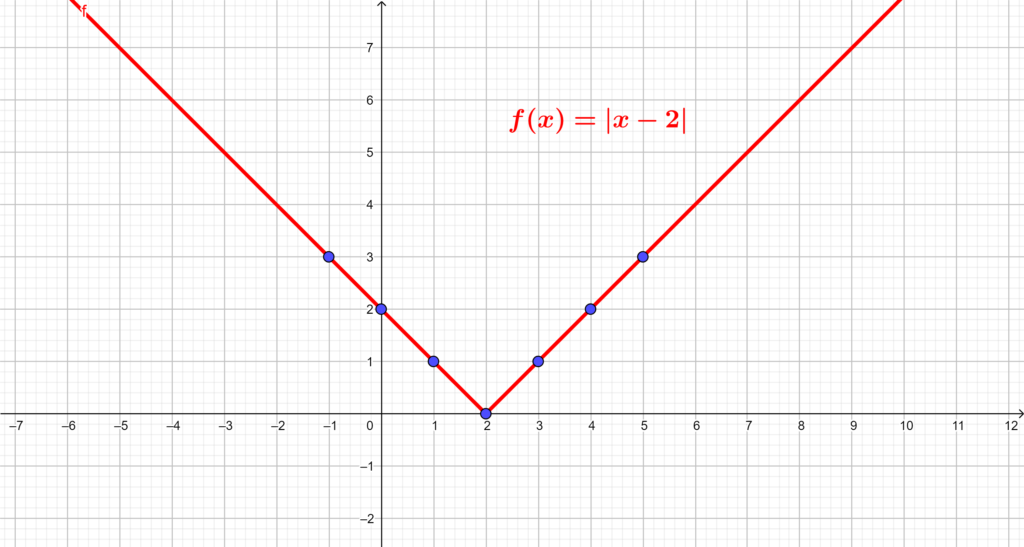
Para mostrar como construir o gráfico da função modular, vamos considerar a função do exemplo anterior: .

Já vimos que essa função pode ser escrita como:

$f(x) = |x-2| = \left\{\begin{matrix} \: \: \: \: (x - 2), \: se\: x >2\\ \: \: \: \: \: \: \: 0, {\color{White} 1111} se\: x =2 \\ -(x-2), \: se\: x <2 \end{matrix}\right.$

Isso significa que a função é uma reta crescente, , para valores maiores que 2, intercepta o eixo das abscissas no ponto , e é uma reta decrescente, , para valores menores que 2.