Funções trigonométricas – Seno, cosseno e tangente
Entenda o que é o círculo trigonométrico e conheça as principais funções trigonométricas: seno, cosseno e tangente.
As funções trigonométricas são funções que possuem um padrão de repetição, ou seja, o comportamento da função se repete após um período. Por isso, tais funções são funções periódicas.
As principais funções periódicas são:
- Função seno
- Função cosseno
- Função tangente
O período dessas três funções se limita a uma volta completa no círculo trigonométrico.
Círculo trigonométrico
O círculo trigonométrico é uma circunferência de raio 1, centrada no ponto (0,0) do plano cartesiano. Essa circunferência é usada para a representação de ângulos e radianos.
No círculo trigonométrico, o eixo x é chamado de eixo dos cossenos e o eixo y de eixo dos senos.
Qualquer ângulo está associado a um ponto P(x, y) da circunferência, sendo que:
- A abscissa do ponto P é o cosseno (
);
- A ordenada do ponto P é o seno (
).
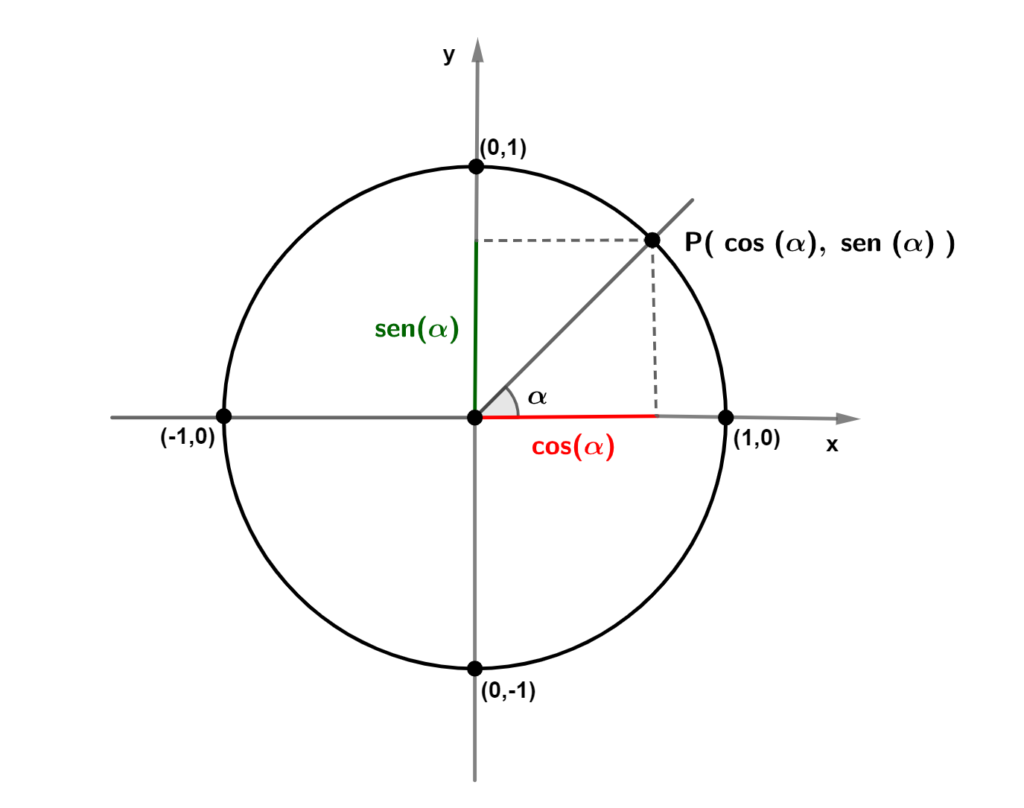
, vamos ter um ponto P marcado na circunferência.
Considere, por exemplo, um ângulo de 30º. Temos que:
e
.
Então, associado ao ângulo de 30º, teremos no círculo trigonométrico, o ponto
P( cos(), sen (
) ) =
.
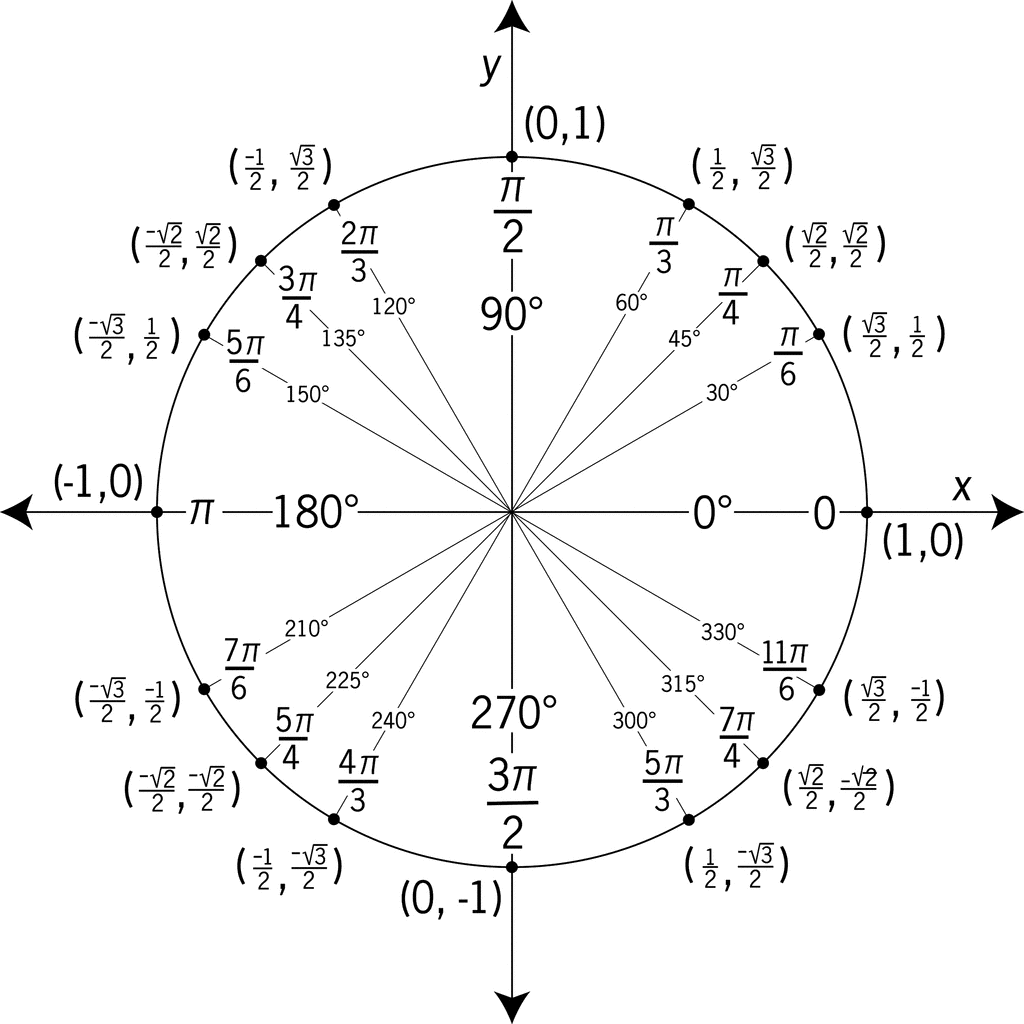
Veja a seguir, como fica o círculo trigonométrico considerando os ângulos notáveis e seus respectivos pontos.
Função seno
Definição: A função seno é definida como a função , que associa a cada número real
, o seu seno.
Domínio: O domínio da função seno é o conjunto dos números reais.
Imagem: A imagem da função seno é o intervalo [-1, 1], ou seja, .
Paridade: A função é uma função ímpar, pois
Período: O período da função seno é , ou seja, é uma volta completa no círculo trigonométrico.
Gráfico da função seno
Considerando apenas os valores de x entre 0 e , que é o período da função, o gráfico da função
é:
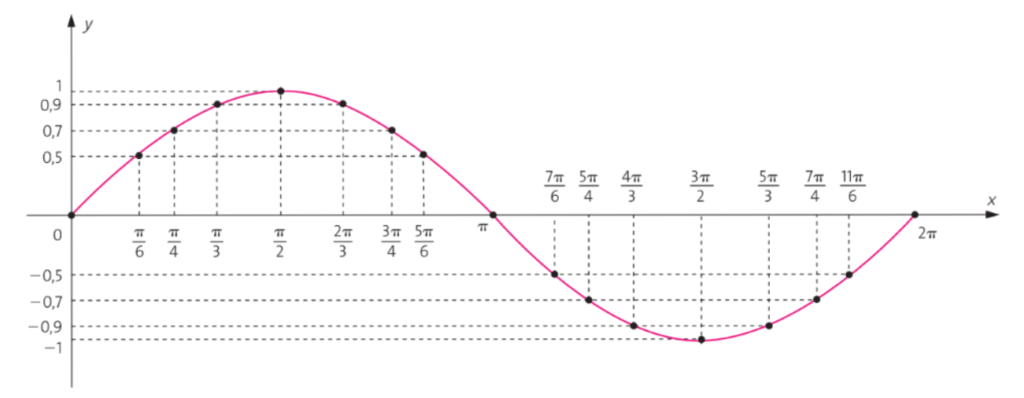
Essa curva é chamada de senóide e corresponde a uma volta completa no círculo trigonométrico.
Observe que os radianos são marcados no eixo x e os pontos da circunferência no eixo y. Através desse gráfico, podemos visualizar o sinal e o comportamento da função seno.
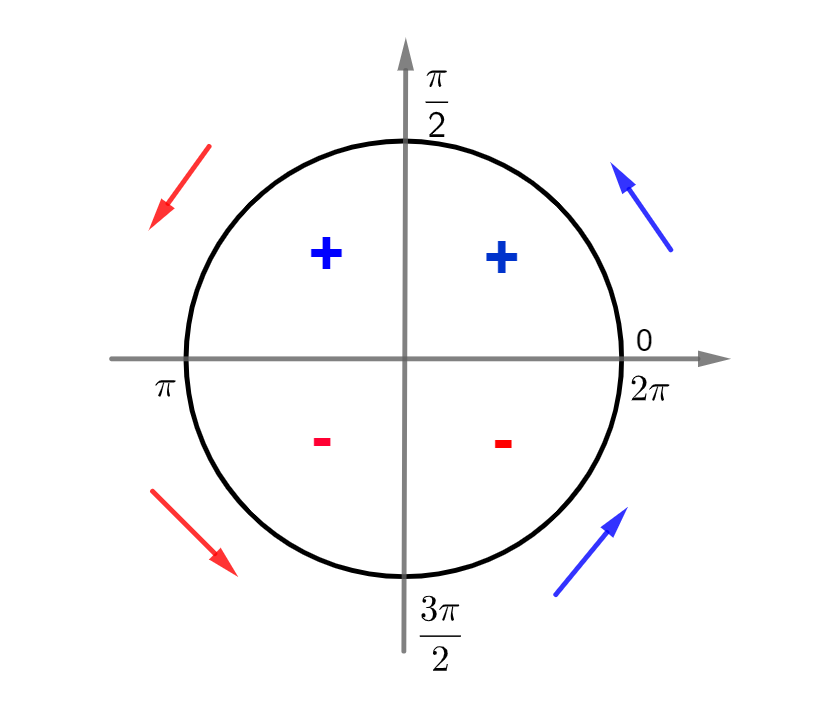
Sinal da função seno:
- Positiva (+) de 0 a
.
- Negativa (–) de
a 2
;
Comportamento da função seno:
- Crescente (⇑) de 0 a
;
- Decrescente de (⇓) de
a
;
- Crescente (⇑) de
a 2
.
Projetando essas informações no círculo trigonométrico, podemos ver o que acontece com a função seno em cada quadrante do plano cartesiano:
Função cosseno
Definição: A função cosseno é definida como a função , que associa a cada número real
, o seu cosseno.
Domínio: O domínio da função cosseno é o conjunto dos número reais.
Imagem: A imagem da função cosseno é o intervalo [-1, 1], ou seja, .
Paridade: A função é uma função par, pois
.
Período: O período da função cosseno é , ou seja, é uma volta completa no círculo trigonométrico.
Gráfico da função cosseno
Considerando apenas os valores de x entre 0 e , que é o período da função, o gráfico da função
é:
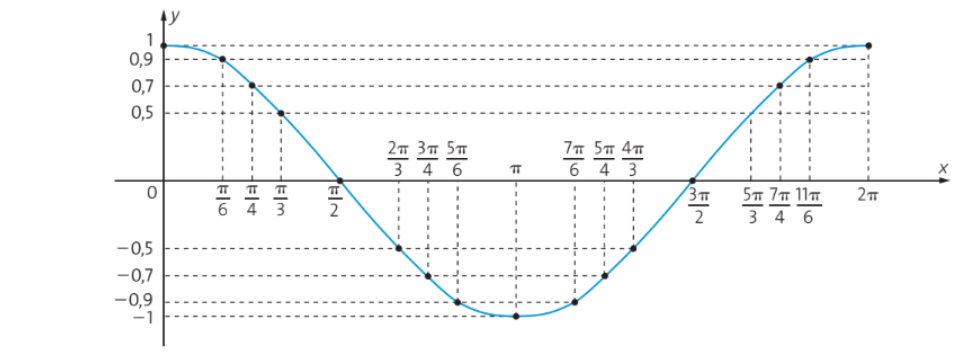
Essa curva é chamada de cossenóide.
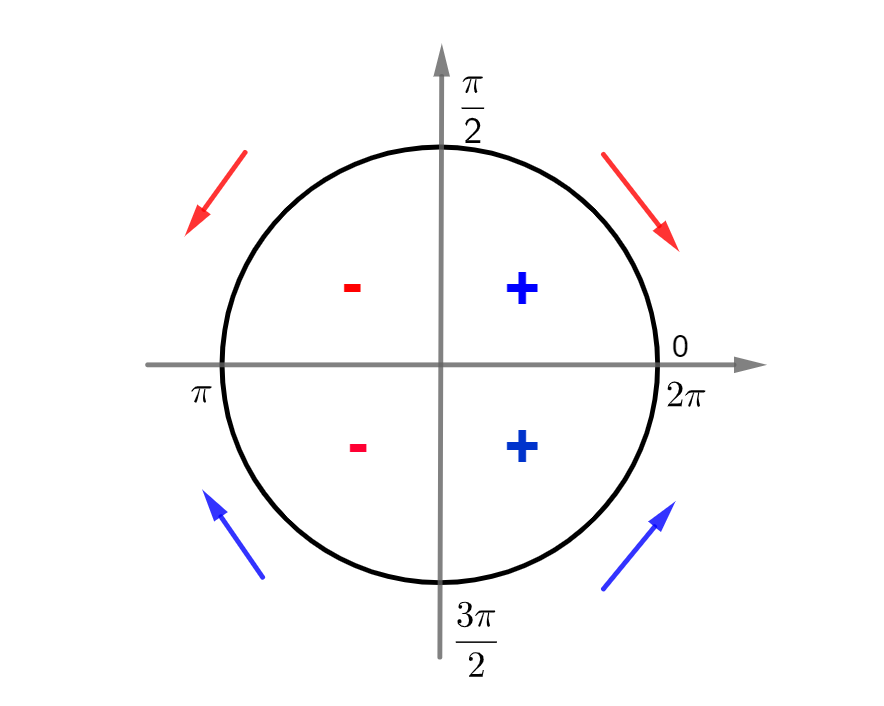
Sinal da função cosseno:
- Positiva (+) de 0 a
;
- Negativa (–) de
a
;
- Positiva (+) de
a 2
.
Comportamento da função cosseno:
- Decrescente de (⇓) de 0 a
;
- Crescente (⇑) de
a 2
.
Projetando essas informações no círculo trigonométrico, podemos ver o que acontece com a função cosseno em cada quadrante do plano cartesiano:
Função tangente
Definição: A função tangente é definida como a função f que associa a tangente de cada número real , com
.
Domínio: O domínio da função tangente é o conjunto:
Imagem: A imagem da função tangente é conjunto dos números reais.
Paridade: A função é uma função ímpar, pois
.
Período: O período da função tangente é , ou seja, é metade da volta no círculo trigonométrico.
Cada curva é chamada de tangentóide.
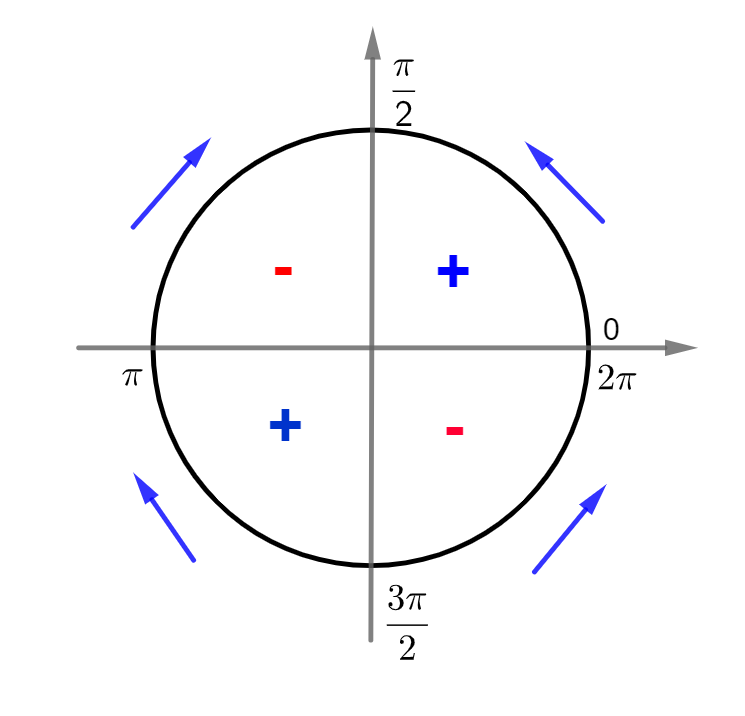
Sinal da função tangente:
- Positiva (+) de 0 a
;
- Negativa (–) de
a
.
- Positiva (+) de
a
;
- Negativa (–) de
a 2
.
Comportamento da função tangente:
- Crescente (⇑) de 0 a 2
, ou seja, em todo o círculo trigonométrico.
Projetando essas informações no círculo trigonométrico, podemos ver o que acontece com a função tangente em cada quadrante do plano cartesiano:
Você também pode se interessar:
- Teorema de Pitágoras – História, fórmula, Triângulo Pitagórico
- Exercícios sobre Teorema de Pitágoras
- Relações métricas no triângulo retângulo


Os comentários estão fechados, mas trackbacks E pingbacks estão abertos.