Números complexos
O números complexos são formados por uma parte imaginária que surgiu da necessidade de calcular raízes de números negativos. Aprenda a forma conjugada desses números, como fazer operações entre eles e muito mais.
Os números complexos são mais abrangentes que os números reais, eles são formados por uma parte real e uma parte imaginária.
A parte imaginária surgiu da necessidade de calcular raízes de números negativos.
Por exemplo, como calcular ?
Mas quanto é ? No conjunto dos números reais, não temos essa resposta, por isso foi criada a unidade imaginária.
Unidade imaginária
A unidade imaginária é representada pela letra e tem valor igual a
, ou seja,
Assim, no cálculo de , temos que:
Então, dizemos que é um número que pertence ao conjunto dos números complexos (
), sendo
um número imaginário.
Podemos calcular o quadrado da unidade imaginária ,veja:
Forma algébrica de um número complexo
Qualquer número complexo pode ser escrito na forma algébrica:
Em que:
-
são números reais;
- O número
é chamado de parte real e indicamos
;
- O número
é chamado de parte imaginária e indicamos
.
Exemplos:
Quando a parte real é igual a zero, o número é chamado de número imaginário puro.
Conjugado de um número complexo
O conjugado de um número complexo é dado por:
Ou seja, para obter o conjugado de um número, basta trocar o sinal da parte imaginária.
Exemplos:
Igualdade entre números complexos
Dois números complexos são iguais quando possuem a mesma parte real e a mesma parte imaginária.
Então, considerando dois números complexos e
, eles só serão iguais se
e
.
Operações com números complexos
Podemos fazer operações com números complexos tanto de adição quanto de subtração, multiplicação e divisão, assim como fazemos entre outros tipos de números.
Adição de números complexos
Para fazer a adição entre números complexos, soma-se parte real com parte real, e parte imaginária com parte imaginária.
Exemplo: Se e
, qual o valor de
?
- Soma das partes reais:
- Soma das partes imaginárias:
Então, .
Também podemos expressar esse cálculo da seguinte forma:
Subtração de números complexos
Para fazer a subtração entre números complexos, subtrai-se parte real de parte real e parte imaginária de parte imaginária.
Exemplo: Se e
, qual o valor de
?
- Subtração das partes reais:
- Subtração das partes imaginárias:
Então, .
Também podemos expressar esse cálculo da seguinte forma:
Multiplicação de números complexos
Para fazer a multiplicação entre números complexos, utiliza-se a propriedade distributiva: multiplica-se cada termo do primeiro fator por cada termo do outro fator.
Exemplo: Se e
, qual o valor de
?
Na quarta linha usamos o fato de que
.
Divisão de números complexos
Para fazer a divisão de um número complexo por um número complexo
, basta fazer:
Em que é o conjugado de
.
Exemplo: Se e
, qual o valor de
?
Você também pode se interessar:

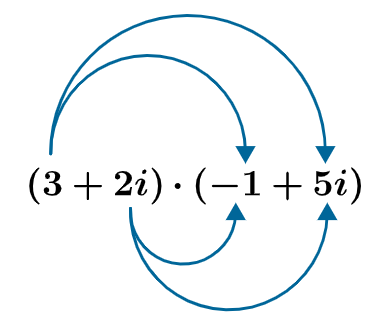
Os comentários estão fechados, mas trackbacks E pingbacks estão abertos.