Números primos
Nesse post você vai aprender o que são números primos, quais são eles e um método simples para achar os números primos entre 1 e 1000.
Os números primos são aqueles que possuem apenas dois divisores: o número 1 e ele mesmo.
Recorde que os divisores são aqueles números para os quais obtemos uma divisão com resto igual a zero.
Assim, o número 7 é um exemplo de número primo, pois seus divisores são apenas o 1 e o próprio 7. Já o número 8 não é um número primo, pois seus divisores são: 1, 2, 4 e 8.
Números primos entre 1 e 100
Existem infinitos números primos. Os 25 primeiros números primos estão entre 1 e 100, são eles:
2, 3, 5, 7,
11, 13, 17, 19,
23, 29, 31, 37, 41, 43, 47,
53, 59, 61, 67, 71, 73, 79,
83, 89 e 97.
Observações:
- O número 1 não é primo, pois só possui um divisor, que é ele mesmo;
- O número 2 é o único número par que é primo.
Decomposição em fatores primos
Qualquer número que não é primo, exceto o número 1, pode ser escrito como uma multiplicação de números primos. Isso é o que chamamos de decomposição em fatores primos.
Para decompor um número em fatores primos:
- Dividimos o número por seu menor divisor primo;
- Repetimos esse processo até obter quociente 1.
O menor número primo é o número 2. Vamos sempre tentar dividir por ele. Se não der, passamos para o próximo número que é o 3, e assim por diante.
Exemplo: Fazer a decomposição do número 12 em fatores primos.
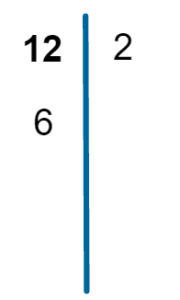
O número 2 é um divisor de 12? Sim. Então dividimos 12 por 2:
E representamos da seguinte forma:
Agora, temos o número 6. O número 2 é um divisor de 6? Sim. Então dividimos 6 por 2:
E representamos da seguinte forma:
Agora, temos o número 3. O número 2 é um divisor de 3? Não.
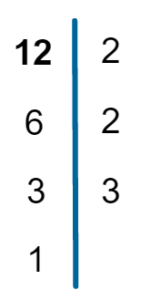
E o número 3, que é o próximo número primo, é um divisor de 3? Sim. Então dividimos 3 por 3:
E representamos da seguinte forma:
Chegamos no número 1. Então, terminamos a decomposição do número 12 em fatores primos e podemos escrever:
E representamos da seguinte forma:
Ou seja, o número 12 foi escrito como uma multiplicação de fatores primos (2 e 3). Dizemos que essa é a forma fatorada do número 12.
Exemplo: Fazer a decomposição do número 110 em fatores primos.
Seguindo o mesmo procedimento do exemplo anterior, em cada etapa, verificamos se o 2 é divisor. Se for, dividimos. Se não for, passamos para o número 3. Depois, passamos para o número 5, depois 7, 11 e assim por diante.
E já podemos usar a representação diretamente:
Crivo de Eratóstenes – Números primos entre 1 e 1000
O Crivo de Eratóstenes é um método criado pelo grego Eratóstenes (276-194 a. C.) para encontrar os números primos entre 1 e 1000.
O método consiste em escrever os números de 1 a 1000 e ir riscando os números que não são primos:
- Risca o número 1;
- Risca os múltiplos de 2, exceto o próprio 2;
- Risca os múltiplos de 3, exceto o próprio 3;
E assim por diante até riscar os múltiplos de 31. No final, os números que não foram riscados são os números primos.
Veja como isso é feito, considerando os números de 1 a 50:
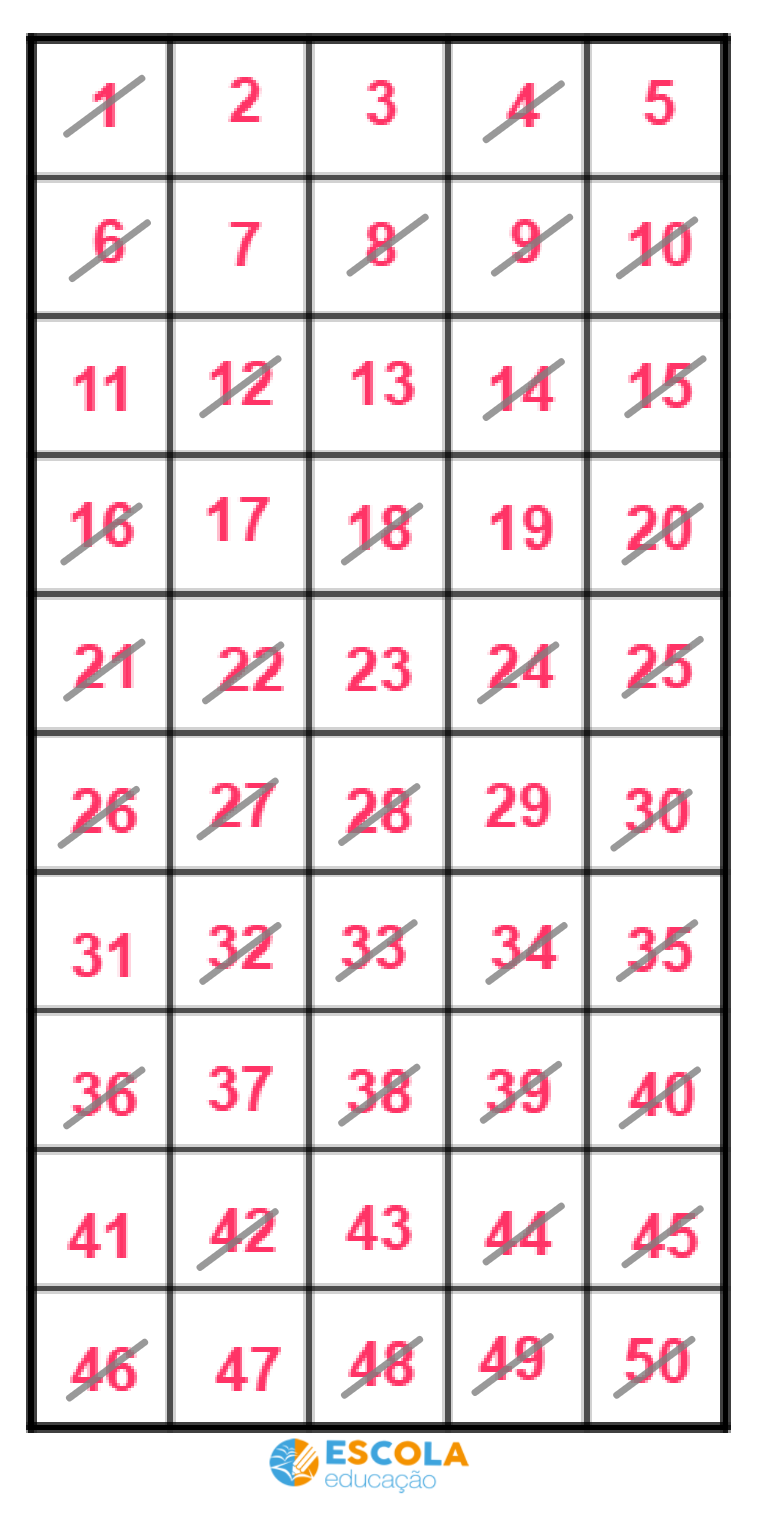
Leia também:

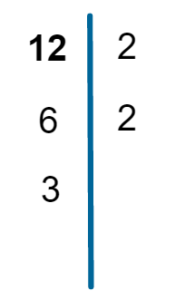
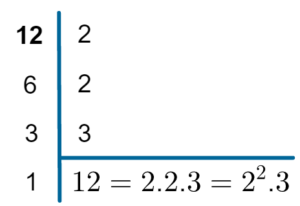
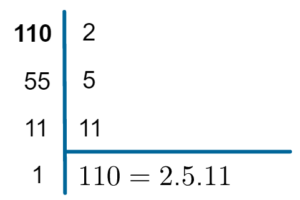
Os comentários estão fechados, mas trackbacks E pingbacks estão abertos.