Perpendicularidade

Em geometria, perpendicularidade é uma palavra que se associa à formação de ângulos retos (90°) quando duas figuras geométricas se interceptam, isto é, se cruzam.

Essas figuras geométricas podem ser, por exemplo, duas retas, uma reta e um plano ou dois planos.

Retas perpendiculares

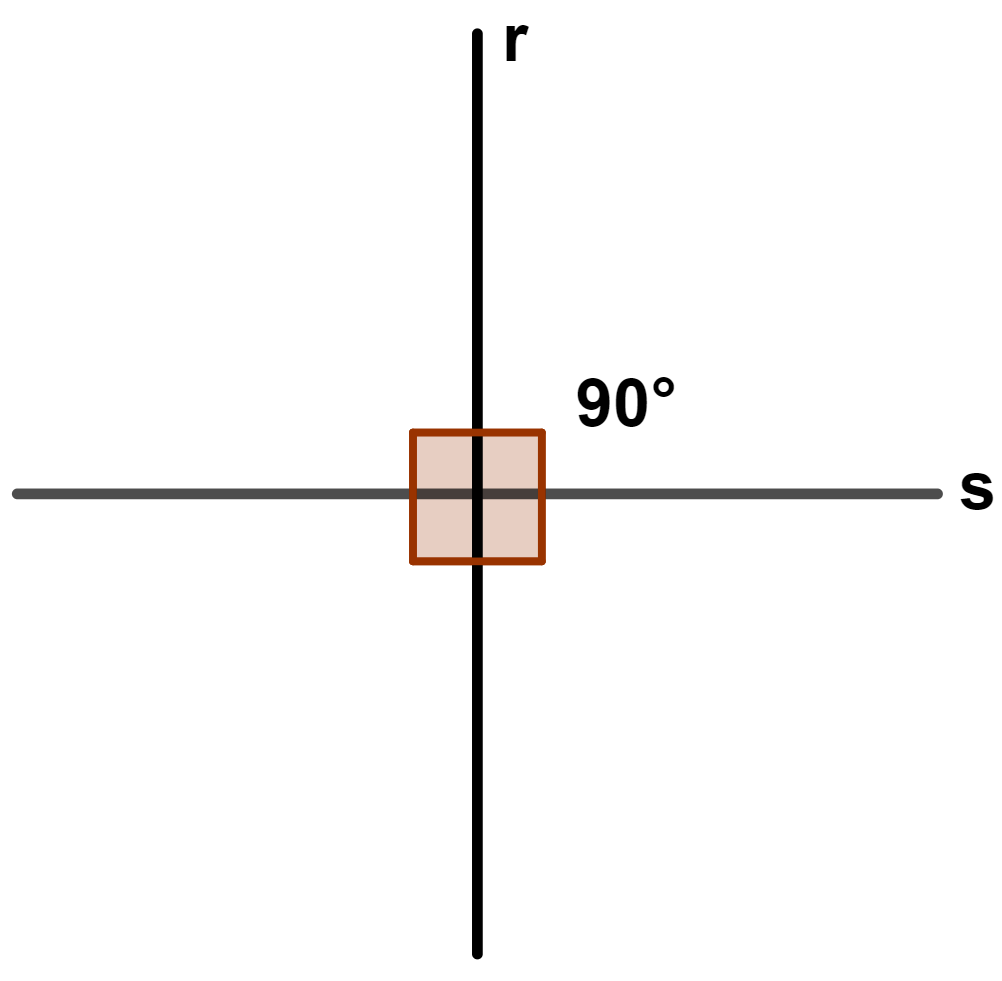
No cruzamento entre duas retas (não coincidentes) sempre são formados quatro ângulos que podem ter medidas variadas de acordo com a posição das retas. Mas, quando os ângulos formados são ângulos retos, as retas são ditas perpendiculares.

Portanto, retas perpendiculares são retas que se cruzam em um único ponto formando ângulos retos.

Na figura, as retas r e s são perpendiculares. Utiliza-se a seguinte notação para indicar a perpendicularidade entre as retas: r ⊥ s.

Reta e plano perpendiculares

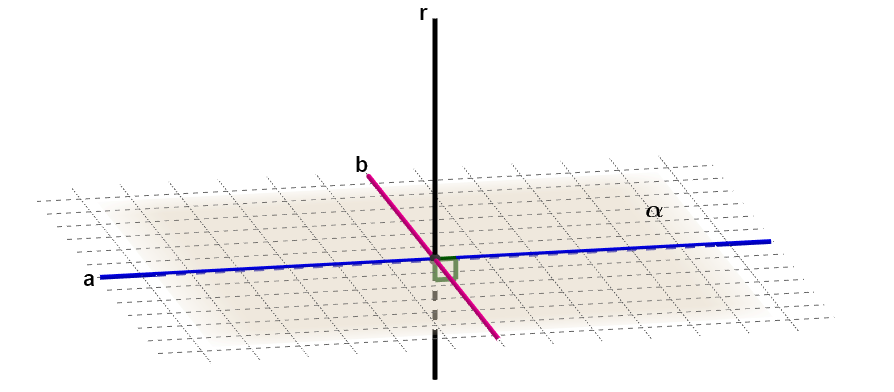
Quando uma reta cruza um plano em um único ponto formando ângulos retos com pelo menos duas retas que pertencem ao plano, então, a reta e o plano são perpendiculares.

Na figura, a reta r é perpendicular às retas a e b do plano , então, a reta r é perpendicular ao plano . Utilizamos a seguinte notação: r ⊥ .

Planos perpendiculares

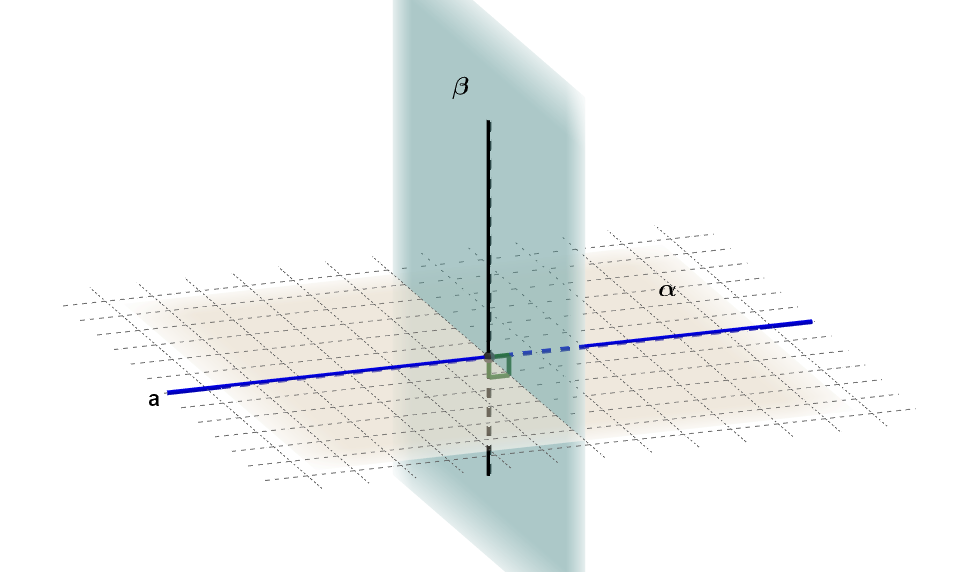
Quando dois planos se cruzam e uma reta de um dos planos é perpendicular ao outro plano, então, são planos perpendiculares.

Na figura, o plano  é perpendicular a reta a do plano , então, o plano  e o plano  são perpendiculares. Utiliza-se a seguinte notação: .

Você também pode se interesse:

• Retas paralelas
• Reta, semirreta e segmento de reta
• Ponto médio de um segmento de reta