Plano de aula – Propriedades dos quadriláteros – 8º ano do Ensino Fundamental

Os quadrados, retângulos e losangos são figuras planas comuns e de grande importância na geometria, elas se caracterizam como quadriláteros, por possuírem quatro lados cada. Além disso, outra característica dessas três figuras, é que são classificadas como paralelogramos.

Os paralelogramos possuem os dois lados opostos paralelos e algumas propriedades bastante relevantes. Essas propriedades podem ser demonstradas a partir da congruência de triângulos.

Para ajudar você a ministrar esse conteúdo, preparamos um plano de aula sobre propriedades dos quadriláteros, conforme a habilidade EF08MA14 da Base Nacional Comum Curricular (BNCC).

Plano de aula – Propriedades dos quadriláteros

TEMA: Propriedades dos quadriláteros

HABILIDADES DA BNCC: (EF08MA14) Demonstrar propriedades de quadriláteros por meio da identificação da congruência de triângulos.

TEMPO SUGERIDO: 2 horas e 30 minutos (3 aulas de 50 minutos)

OBJETIVOS:

• Entender que as diagonais do paralelogramo dividem a figura em triângulos congruentes;
• Demonstrar as propriedades dos paralelogramos a partir da congruência de triângulos.

MATERIAL NECESSÁRIO:

• Atividade impressa;
• Lápis e borracha;
• Canetas coloridas;
• Régua;
• Cola;
• Transferidor.

DESENVOLVIMENTO:

Inicie a aula relembrando o que são triângulos congruentes, pois o objetivo é que os alunos compreendam as três propriedades dos paralelogramos a partir da congruência de triângulos.

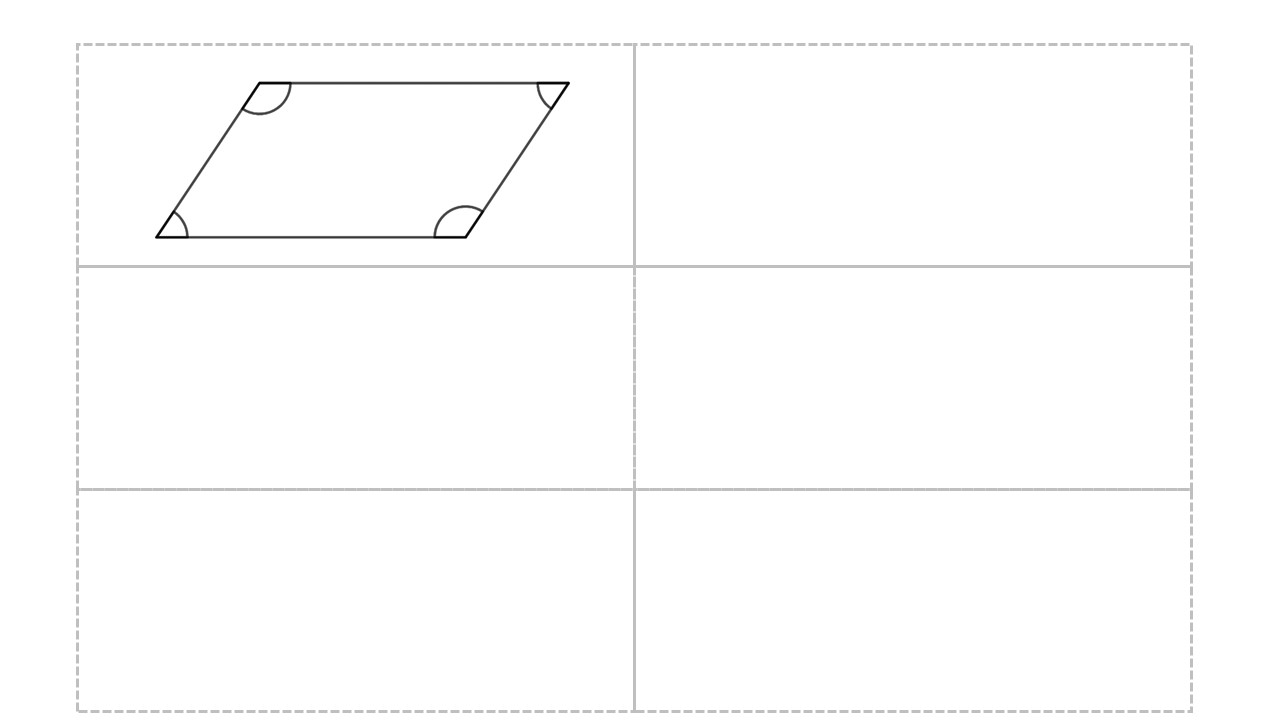
Entregue a atividade impressa para que cada aluno recorte o paralelogramo e, a partir dele e do uso da régua, construa réplicas em cada cartão da folha.

Clique aqui para baixar a atividade em PDF!

Peça para recortarem todos os cartões com os paralelogramos feitos.

1ª propriedade

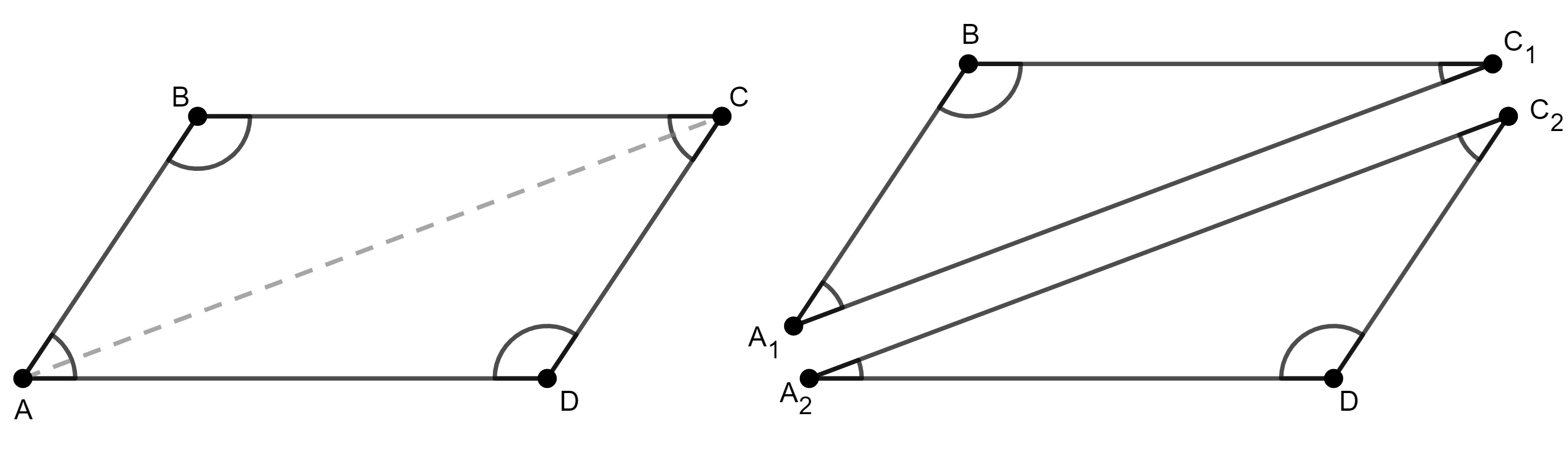
Em um dos cartões, os alunos vão marcar os vértices A, B, C e D, traçar a diagonal  e recortar, formando dois triângulos, conforme é apresentado na figura abaixo.

Em seguida, eles precisam observar os dois triângulos obtidos e comparar as medidas dos lados e dos ângulos deles, sobrepondo as figuras.

Fazendo isso, os alunos poderão observar que os triângulos são congruentes. A partir disso, pergunte o que eles podem concluir a respeito dos lados do paralelogramo.

A ideia é que eles percebam que os lados opostos  e  e os lados opostos  e  do paralelogramo são congruentes.

Peça para que anotem a primeira propriedade no caderno e colem um paralelogramo (inteiro) abaixo, marcando os lados opostos congruentes com duas cores diferentes de caneta.

2ª propriedade

Ainda com os recortes anteriores, pergunte aos alunos o que eles podem dizer em relação aos ângulos  e  dos triângulos congruentes.

Após eles identificarem que esses dois ângulos são congruentes, pergunte o que eles podem dizer sobre os ângulos  e  do paralelogramo.

Peça para usarem o transferidor para obter a medida de cada ângulo, confirmando que esses ângulos têm a mesma medida.

Em seguida, eles vão utilizar outra réplica do paralelogramo ABCD e traçar a diagonal . Pergunte o que eles concluem sobre as medidas dos ângulos  e .

Depois, peça para medirem esses ângulos, também com o transferidor, anotarem a segunda propriedade no caderno e colarem um paralelogramo (inteiro) abaixo, marcando os ângulos opostos congruentes com duas cores diferentes.

3ª propriedade

Em outra réplica, os alunos vão traçar as duas diagonais, e , do paralelogramo ABCD.

Peça que recortem os quatro triângulos formados e os observem, buscando identificar quais triângulos são congruentes. Diga para sobreporem as figuras para ajudar nessa identificação.

O objetivo é que eles vejam que os triângulos AMD e BMC são congruentes e que os lados  e  são de mesmo tamanho. Logo, o ponto M é o ponto médio da diagonal .

De modo equivalente, eles irão ver que M é o ponto médio da diagonal .

Por fim, eles vão anotar a terceira propriedade no caderno e colar um paralelogramo (inteiro) abaixo, marcando as diagonais e destacando o ponto de encontro como o ponto médio.

AVALIAÇÃO:

A avaliação poderá ser feita a partir da observação dos alunos durante a aula e a realização das atividades.

Para baixar esse plano em PDF, clique aqui!

Você também pode se interessar:

• Plano de aula – Bissetriz e mediatriz – 8º ano do Ensino Fundamental
• Plano de aula – Polígonos regulares – 8º ano do Ensino Fundamental
• Plano de aula – Eventos dependentes – 9º ano do Ensino Fundamental