Projeção ortogonal

As projeções ortogonais são como as sombras de objetos que vemos, ao meio-dia, formadas no chão em dias ensolarados. A palavra ortogonal significa perpendicular, ou seja, está relacionada com a formação de ângulos de 90° entre figuras geométricas.

Confira uma definição mais formal do que seria uma projeção ortogonal:

A projeção ortogonal de uma figura geométrica em um plano corresponde ao conjunto de pontos formados no plano a partir da projeção ortogonal de cada ponto da figura no plano.

É importante ressaltar que, assim como uma sombra nem sempre é fiel ao formato do objeto, a projeção ortogonal no plano não precisa ser igual à figura geométrica da qual deriva a projeção.

Para compreender melhor sobre projeção ortogonal, veja como são as projeções de figuras fundamentais da geometria: ponto e segmento de reta.

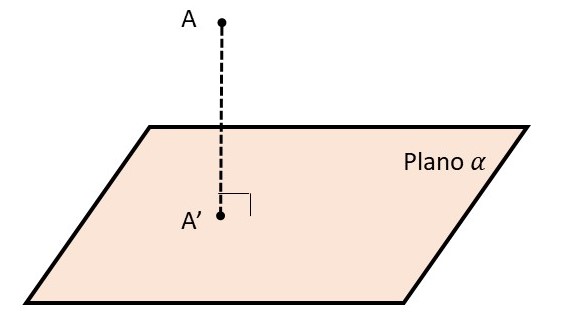
Projeção ortogonal de um ponto sobre um plano

A projeção ortogonal de um ponto sobre um plano é um ponto também, de forma que se o ponto fora do plano e o ponto projetado no plano forem ligados, obtém-se um segmento de reta que é perpendicular ao plano.

Projeção ortogonal de um segmento de reta sobre um plano

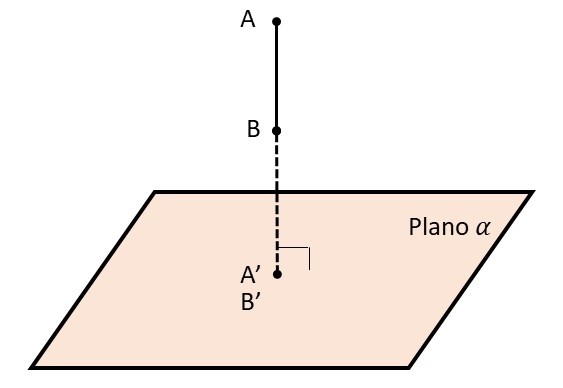
A projeção ortogonal de um segmento de reta sobre um plano pode ser um ponto ou um outro segmento de reta.

Será um ponto se o segmento de reta for perpendicular ao plano:

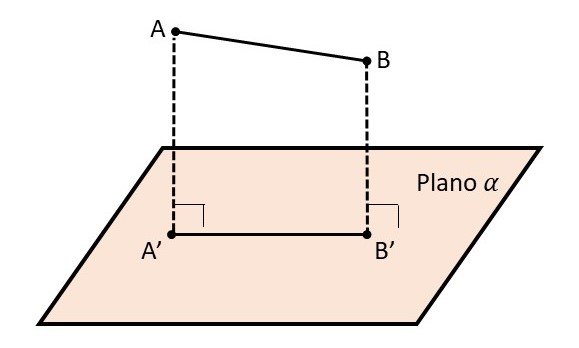
Será outro segmento de reta se o segmento de reta não for perpendicular ao plano:

Dessa forma, você já pode imaginar como seria a projeção ortogonal de polígonos como triângulos, quadrados, retângulos, hexágonos, que são figuras formadas apenas por segmentos de retas.

Você também pode se interessar:

• Retas paralelas
• Área dos polígonos
• Medidas de volume e capacidade