Área do hexágono

Aprenda a calcular a área do hexágono regular a partir da medida do lado e do apótema. Veja, também, como calcular a área de um hexágono irregular.

Por Elainy Marciano Publicado em 28/08/2020 - 22:01

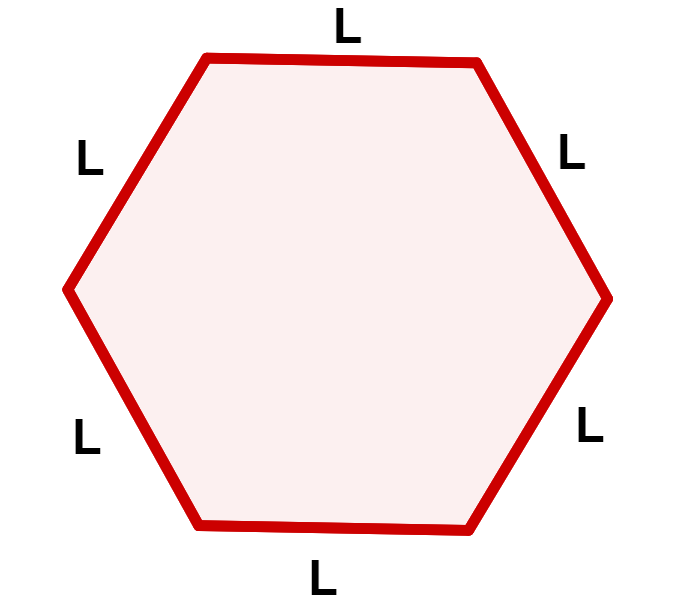
O hexágono é o nome do polígono formado por seis segmentos de reta. Cada um desses segmentos é chamado de lado do hexágono.

Quando os lados do hexágono são todos do mesmo tamanho e os ângulos internos têm a mesma medida, o hexágono é regular. Caso contrário, o hexágono é irregular.

Veja mais

O limite numérico: até onde vai o maior número que conhecemos?

Reditec debate ensino profissional e tecnológico

Área do hexágono regular

O hexágono regular possui os seis lados do mesmo tamanho e os seis ângulos internos de mesma medida.

A fórmula da área do hexágono regular é:

$\dpi{120} \boldsymbol{\mathrm{A_H = \frac{3}{2}\cdot L^2\sqrt{3}}}$

Demonstração:

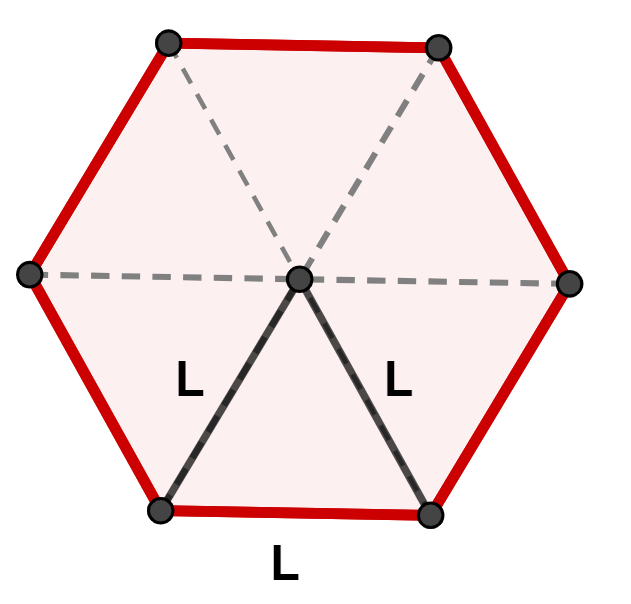
Esse tipo de hexágono pode ser dividido em seis triângulos equiláteros, que são triângulos cujos lados são todos iguais.

Dessa forma, calcular a área do hexágono regular de lado L é o mesmo que calcular a área de um triângulo equilátero de lado L e multiplicar o resultado por seis.

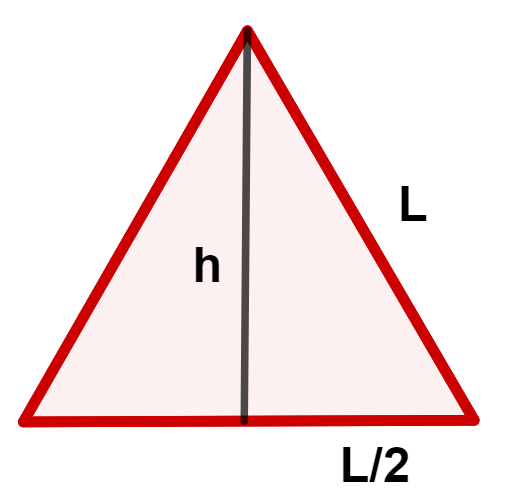
Para calcular a área de um triângulo qualquer, multiplicamos a base (b) pela altura (h) e depois dividimos por dois.

$\dpi{120} \mathrm{A_T = \frac{b\cdot h}{2}}$

Já sabemos que b = L, mas e quanto à altura?

Observe que a altura divide o triângulo equilátero em dois triângulos retângulos. Assim podemos utilizar o teorema de Pitágoras para calcular a sua altura (um dos catetos do triângulo).

$\dpi{120} \mathrm{L^2 = h^2 + \bigg(\frac{L}{2}\bigg)^2}$

Isolando h nessa equação, temos uma expressão para a altura do triângulo em função do lado:

$\dpi{120} \mathrm{h = \frac{\sqrt{3}}{2}L}$

Então, aplicando essa expressão na fórmula da área do triângulo, obtemos uma fórmula para calcular a área do triângulo equilátero apenas com a medida do lado L.

$\dpi{120} \mathrm{A_T = \frac{b\cdot h}{2} = \frac{b\cdot \frac{\sqrt{3}}{2}L}{2}}$

$\dpi{120} \Rightarrow \mathrm{A_T = \frac{L^2\sqrt{3}}{4}}$

Por fim, a área do hexágono corresponde a seis vezes a área desse triângulo:

$\dpi{120} \mathrm{A_H = 6\cdot A_T}$

$\dpi{120} \Rightarrow \mathrm{A_H = 6\cdot \frac{L^2\sqrt{3}}{4}}$

$\dpi{120} \Rightarrow \mathrm{A_H = \frac{3}{2}\cdot L^2\sqrt{3}}$

Área do hexágono regular a partir do apótema

A área do hexágono regular também pode ser obtida a partir da medida do apótema e do perímetro. O apótema é a medida do centro do hexágono até o ponto médio de um dos seus lados.

A fórmula da área do hexágono regular a partir do apótema é:

$\dpi{120} \boldsymbol{\mathrm{A_H = \frac{P}{2}\cdot a}}$

Em que:

P é o perímetro do hexágono (P = 6.L);
a: apótema.

Observe que o apótema corresponde a altura do triângulo equilátero, visto anteriormente. Assim, as duas fórmulas são equivalentes.

Área do hexágono irregular

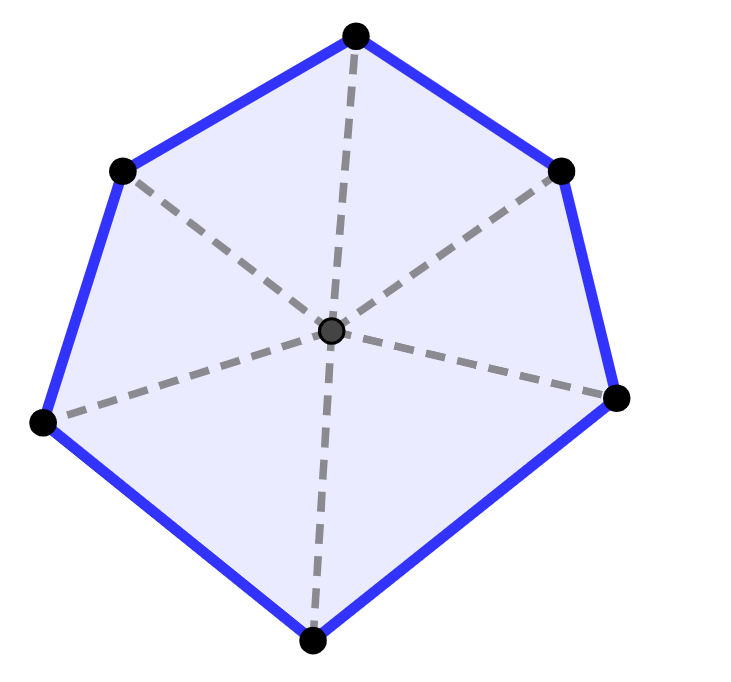
O hexágono irregular possui lados com medidas diferentes e um dos métodos para calcular a área, nesse caso, é fazer a divisão do hexágono em figuras com áreas conhecidas e mais fáceis de calcular.

Veja que o hexágono da figura foi dividido em seis triângulos diferentes. Assim, a área desse hexágono é dada pela soma das áreas dos triângulos.

Nem sempre a divisão resultará em triângulos, podem ser outras figuras geométricas planas.

Você também pode se interessar:

Hexágono Polígono