Reta, semirreta e segmento de reta

Reta, semirreta e segmento de reta são elementos básicos que constituem os estudos de geometria. A ideia de uma reta é bem intuitiva, podemos ter a noção de reta ao olharmos uma corda ou um fio bem esticado.

Os outros dois elementos, semirreta e segmento de reta, são partes de uma reta. A semirreta é uma “reta com início e sem fim”. Já o segmento é uma “reta com início e fim”. Vamos entender melhor sobre cada um desses elementos?!

Reta

Uma reta é uma linha formada por infinitos pontos alinhados, ou seja, uma reta é uma linha que não tem início e não tem fim.

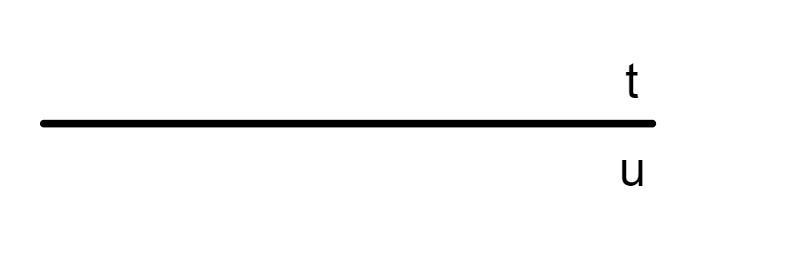
É impossível desenhar uma reta, já que ela é infinita. No entanto, podemos fazer uma representação de uma reta, desenhando apenas um pedaço dela. Utilizamos uma letra minúscula qualquer para indicá-la.

Veja alguns exemplos de representação de retas:

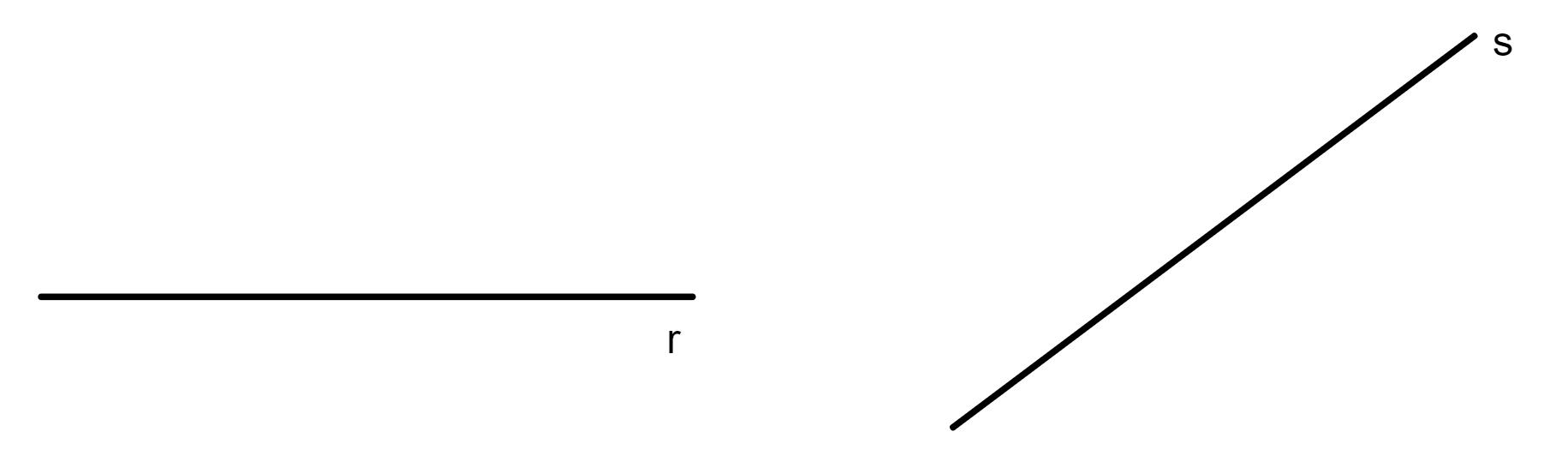
Semirreta

Uma semirreta é uma parte da reta, ela tem início, mas não tem fim. Utilizamos letras maiúsculas para indicar o ponto de início da semirreta e um ponto pelo qual essa semirreta passa.

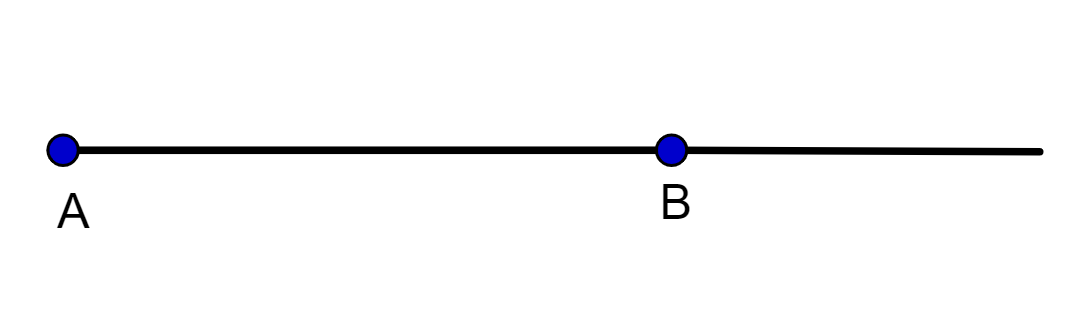
Se a semirreta não tem fim, por que precisamos do ponto B? Lembre-se de que por um único ponto A passam infinitas retas. Então o ponto B serve para identificar sobre qual semirreta estamos falando.

A notação para semirretas é: semirreta 

Segmento de reta

Um segmento de reta é uma parte da reta, ele tem início e fim.

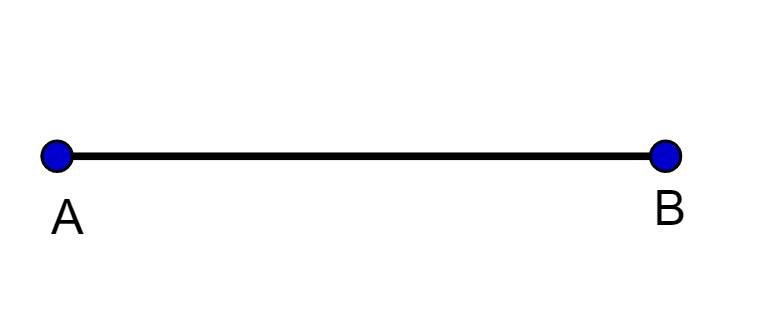
Aqui, os pontos A e B são extremidades do segmento, ou seja, representam o ponto onde começa e onde termina o segmento.

Utilizamos a seguinte notação: segmento de reta .

Posições relativas de duas retas

Duas retas podem ser paralelas, concorrentes (ou secantes) ou coincidentes.

Retas paralelas: são duas retas que nunca se cruzam.

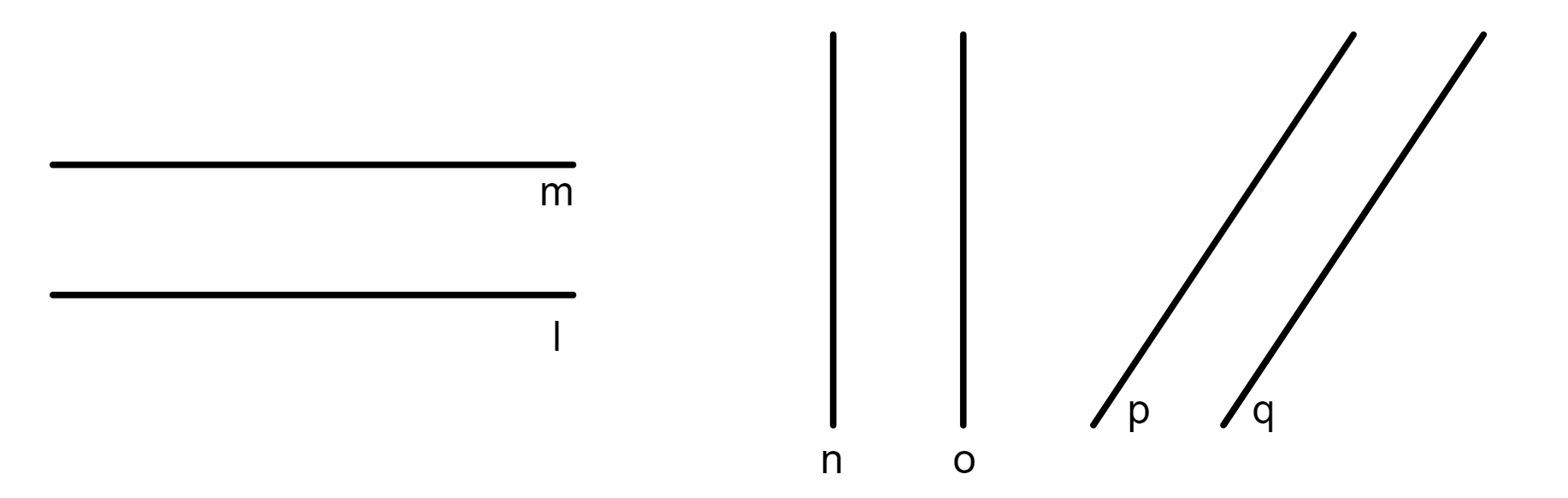
Retas concorrentes: são duas retas que possuem um ponto de cruzamento.

Nem sempre o ponto de cruzamento é evidente na representação de duas retas concorrentes, como é o caso das retas e e f.

Devemos lembrar que as retas são infinitas e imaginar sua continuidade (pontilhado na figura). Se em algum momento essas retas se cruzarem, então elas são concorrentes.

Retas coincidentes: são duas retas que ocupam a mesma posição, como se uma estivesse em cima da outra.

Você também pode se interessar:

• Áreas de figuras planas
• Ângulos – Tipos, classificações e exemplos
• Planificação de sólidos geométricos