Segmentos proporcionais

Entenda o que são segmentos de retas proporcionais, veja exemplos e saiba como interpretar esses conceitos.

Por Elainy Marciano Publicado em 13/11/2020 - 16:28

Quando a razão entre dois segmentos tem o mesmo resultado da razão entre outros dois segmentos, os quatro segmentos de retas envolvidos formam uma proporção. Nesse caso, dizemos que eles são segmentos proporcionais.

Lembre-se que segmentos de retas são partes de uma reta, eles possuem um ponto de origem e um ponto final, portanto, podem ser medidos. É a partir do comprimento dos segmentos que são calculadas as razões entre eles.

Veja mais

O limite numérico: até onde vai o maior número que conhecemos?

Reditec debate ensino profissional e tecnológico

Razão entre dois segmentos de reta

Na matemática, razão é definida como o quociente entre dois números $\dpi{120} a$ e $\dpi{120} b$ , sendo $\dpi{120} b$ diferente de zero. Ela pode ser representada na forma fracionária:

$\dpi{120} \frac{a}{b}\rightarrow Raz\tilde{a}o\, entre \, a \, e\, b$

As razões são, geralmente, utilizadas para comparar valores de uma mesma grandeza, como comparar duas medidas de tempo, distância, altura, largura, temperatura, etc.

A razão entre dois segmentos é a divisão do comprimento de um segmento pelo comprimento do outro segmento.

Exemplo:

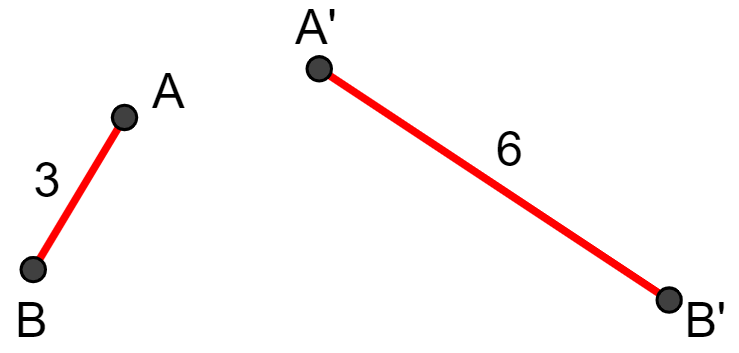
A razão entre os segmentos $\dpi{120} \mathrm{\overline{AB}}$ e $\dpi{120} \mathrm{\overline{A'B'}}$ , de comprimentos 3 e 6, respectivamente, é dada por:

$\dpi{120} \frac{\overline{AB}}{\overline{A'B'}} = \frac{3}{6} = \frac{1}{2} = 0,5$

O resultado da razão é 1/2 ou 0,5. Isso nos diz que o comprimento do segmento $\dpi{120} \mathrm{\overline{AB}}$ é metade do comprimento do segmento $\dpi{120} \mathrm{\overline{A'B'}}$ .

Segmentos proporcionais

Na matemática, quando duas razões têm o mesmo resultado, dizemos que elas formam uma proporção, ou seja, se $\dpi{120} \frac{a}{b}=r$ e $\dpi{120} \frac{c}{d}=r$ , então, temos uma proporção:

$\dpi{120} \frac{a}{b}= \frac{c}{d} = r$ Assim, no caso de segmentos de reta, se o resultado da razão entre dois segmentos é igual ao resultado da razão entre outros dois segmentos, temos segmentos proporcionais.

Exemplo:

Razão entre os segmentos $\dpi{120} \mathrm{\overline{AB}}$ e $\dpi{120} \mathrm{\overline{A'B'}}$ :

$\dpi{120} \frac{\overline{AB}}{\overline{A'B'}} = \frac{3}{6} = \frac{1}{2} = 0,5$

Razão entre os segmentos $\dpi{120} \mathrm{\overline{CD}}$ e $\dpi{120} \mathrm{\overline{C'D'}}$ :

$\dpi{120} \frac{\overline{CD}}{\overline{C'D'}} = \frac{4}{8} = \frac{1}{2} = 0,5$

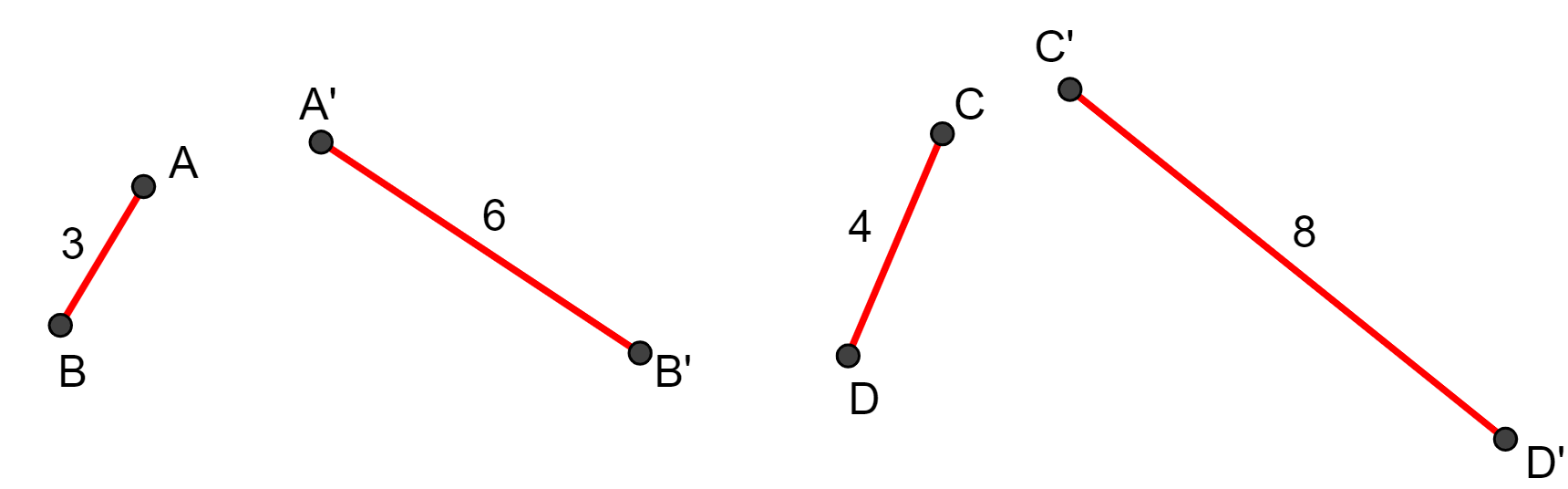
Observe que os resultados das duas razões são iguais a 0,5. Então, os segmentos $\dpi{120} \mathrm{\overline{AB}}$ , $\dpi{120} \mathrm{\overline{A'B'}}$ , $\dpi{120} \mathrm{\overline{CD}}$ e $\dpi{120} \mathrm{\overline{C'D'}}$ , nessa ordem, formam uma proporção, ou seja, são segmentos proporcionais.

Podemos escrever:

$\dpi{120} \frac{\overline{AB}}{\overline{A'B'}} =\frac{\overline{CD}}{\overline{C'D'}} = 0,5$

Isso nos diz que, embora os comprimentos sejam diferentes, nos dois pares de segmentos, o segmento menor tem metade do comprimento do segmento maior, 3 é a metade de 6, assim como 4 é a metade de 8.

Você também pode se interessar:

Geometria plana