Teorema fundamental da semelhança

Entenda o que é o teorema fundamental da semelhança e como ele pode ser aplicado no estudo dos triângulos.

Por Elainy Marciano Publicado em 23/11/2020 - 17:58

O teorema fundamental da semelhança diz respeito à semelhança de triângulos. Por isso, antes de falar sobre o teorema vamos entender o que são triângulos semelhantes.

Em triângulos, a semelhança ocorre quando os ângulos internos correspondentes têm a mesma medida e os lados correspondentes têm medidas proporcionais.

Veja mais

O limite numérico: até onde vai o maior número que conhecemos?

Reditec debate ensino profissional e tecnológico

Lembre-se que semelhança é diferente de congruência, as figuras não precisam ser exatamente iguais para serem semelhantes, elas precisam ser proporcionais.

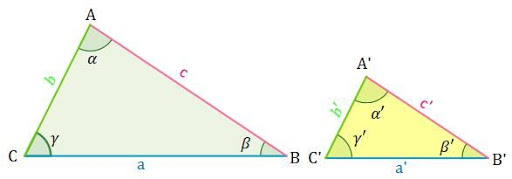
Considere os triângulos ABC e A’B’C’ abaixo:

Para que esses dois triângulos sejam semelhantes, é necessário que:

$\dpi{120} \alpha = \alpha'$ , $\dpi{120} \beta = \beta'$ , $\dpi{120} \gamma = \gamma'$ e $\dpi{120} \frac{\mathrm{a}}{\mathrm{a'}} = \frac{\mathrm{b}}{\mathrm{b'}}=\frac{\mathrm{c}}{\mathrm{c'}}$

No entanto, há algumas condições que, se satisfeitas, já são suficientes para dizermos que os triângulos são semelhantes. Essas condições são conhecidas como casos de semelhança:

Caso AA – Dois ângulos correspondentes têm a mesma medida;
Caso LLL – Três lados correspondentes têm medidas proporcionais;
Caso LAL – Dois lados correspondentes têm medidas proporcionais e o ângulo entre eles de mesma medida.

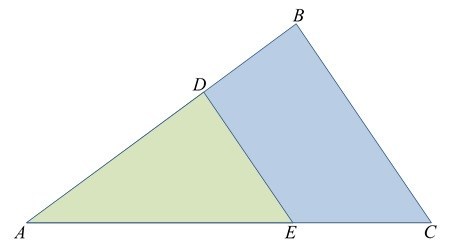
Teorema fundamental da semelhança

O teorema fundamental da semelhança nos diz que, em qualquer triângulo, se desenharmos uma reta paralela a um dos lados do triângulo, de forma que ela intercepte os outros dois lados, então, obtemos outro triângulo que é semelhante ao primeiro.

Exemplo:

Pelo teorema fundamental da semelhança, podemos dizer que os triângulos ABC e ADE são triângulos semelhantes, já que o segmento DE é paralelo ao lado BC e intercepta os lados AB e AC nos pontos D e E, respectivamente.

Agora, vamos entender por que isso acontece, acompanhe uma demonstração desse teorema.

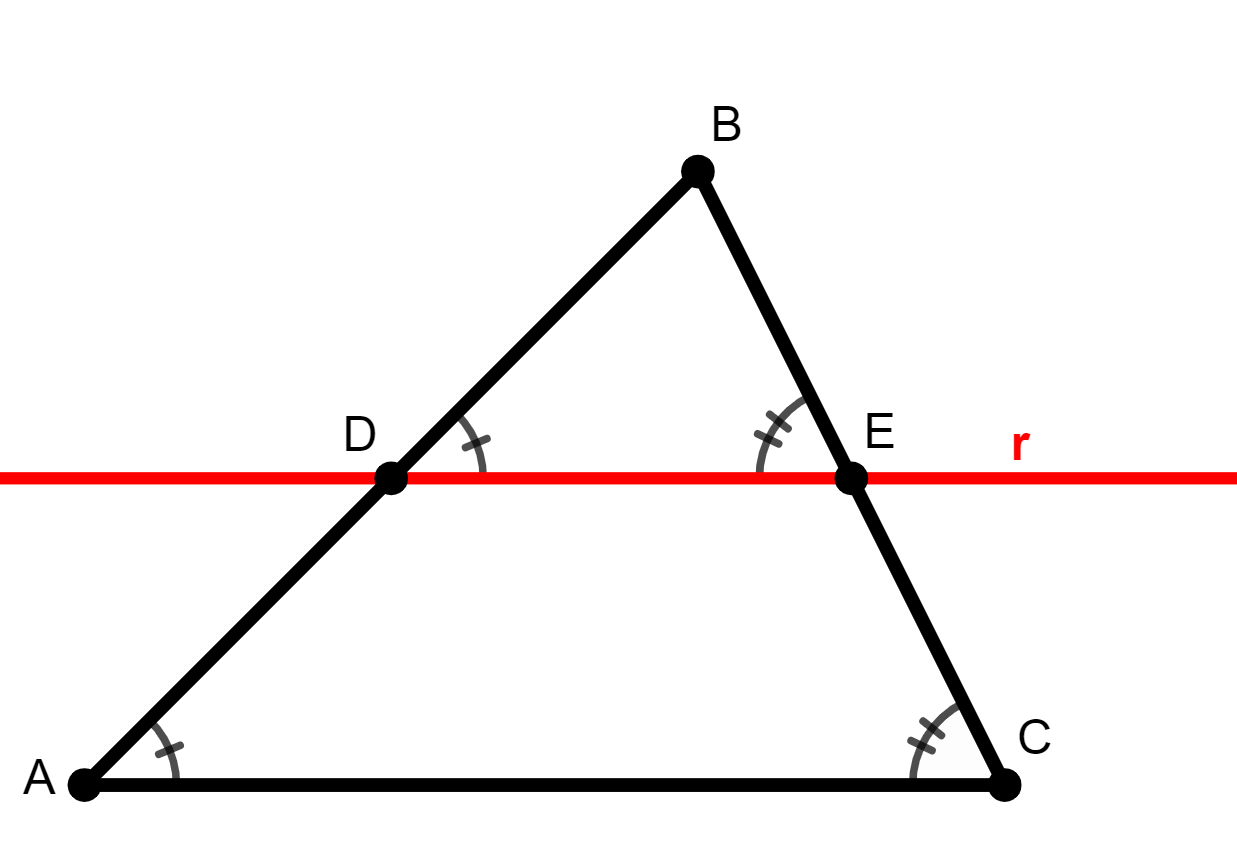
Demonstração:

Em um triângulo qualquer ABC, traçamos uma reta r, paralela ao lado AC e que passa pelo lado AB no ponto D e pelo lado BC no ponto E.

Os ângulos $\dpi{120} \mathrm{\hat{A}}$ e $\dpi{120} \mathrm{\hat{D}}$ são ângulos correspondentes formados por duas retas paralelas e uma reta transversal e, portanto, são congruentes, ou seja, eles têm a mesma medida.

De modo análogo, os ângulos $\dpi{120} \mathrm{\hat{C}}$ e $\dpi{120} \mathrm{\hat{E}}$ também são correspondentes congruentes, eles têm a mesma medida.

Dessa forma, os triângulos ABC e o BDE possuem dois ângulos correspondentes de mesma medida e podemos concluir, pelo caso de semelhança AA, que eles são triângulos semelhantes.

Você também pode se interessar:

Geometria plana Triângulos