Frações equivalentes
Muitos cálculos matemáticos com frações ficam mais simples quando encontramos frações equivalentes. Aprenda tudo sobre elas e saiba como fazer simplificação de fração.
As frações são utilizadas para representar partes de um todo e um fato interessante é que uma mesma porção de um todo pode ser representada por várias frações, que são chamadas de frações equivalentes.
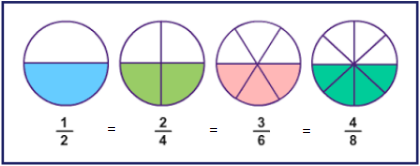
Parece estranho? Não se preocupe, observe a figura a seguir e veja como isso acontece. Cada um dos discos estão pintados pela metade e as frações representam essa metade.
As frações representam a mesma porção do todo, por isso, são chamadas de frações equivalentes e podemos dizer que:
Resumindo:
Como encontrar frações equivalentes?
Para encontrar uma fração equivalente a outra, basta multiplicar ou dividir o numerador e o denominador da fração por um mesmo número, diferente de zero.
Exemplos:
a)
Multiplicando o numerador e o denominador por 2, obtemos a fração equivalente . Assim, temos que:
b)
Dividindo o numerador e o denominador por 3, obtemos a fração equivalente . Desse modo, temos:
Além disso, considerando as frações dos itens (a) e (b), podemos dizer que as frações são equivalentes, ou seja:
Como verificar frações equivalentes
Para verificar se duas ou mais frações são equivalentes, fazemos o caminho inverso, devemos verificar se de uma das frações conseguimos obter a outra através da multiplicação ou divisão do numerador e do denominador por um mesmo número.
Exemplos:
a)
Existe algum número que podemos multiplicar ou dividir os termos da fração e chegar na fração
?
Sim, multiplicando os termos da fração por 3, chegamos na fração
.
Assim, as duas frações são equivalentes.
b)
Existe algum número que podemos multiplicar ou dividir os termos da fração e chegar na fração
?
Não, não existe nenhum número. Então, as duas frações não são equivalentes.
Simplificação de frações
Simplificar uma fração significa escrever uma fração equivalente a ela, mas que tenha termos menores. Assim, o que temos que fazer é dividir o numerador e o denominador da fração por um mesmo número (maior que 1).
Exemplos:
a)
Dividindo os termos da fração por 2, chegamos na fração .
Assim, é a forma simplificada da fração
, e podemos escrever:
b)
Dividindo os termos da fração por 2, chegamos na fração . Mas observe que podemos simplificar ainda mais essa fração, dividindo os termos por 2, outra vez, e chegando na fração
.
Desse modo, temos que:
Quando não conseguimos mais simplificar os termos de uma fração, dizemos que ela é uma fração irredutível.
Você também pode se interessar:

Os comentários estão fechados, mas trackbacks E pingbacks estão abertos.