Área do triângulo usando os ângulos

A área do triângulo pode ser calculada a partir da multiplicação da medida da base pela altura e dividindo esse resultado por dois.

Essa é uma fórmula geral da área do triângulo. No entanto, em muitas situações, a altura do triângulo é desconhecida e deve ser obtida à parte.

Uma das formas de encontrar a altura de um triângulo é a partir das razões trigonométricas.

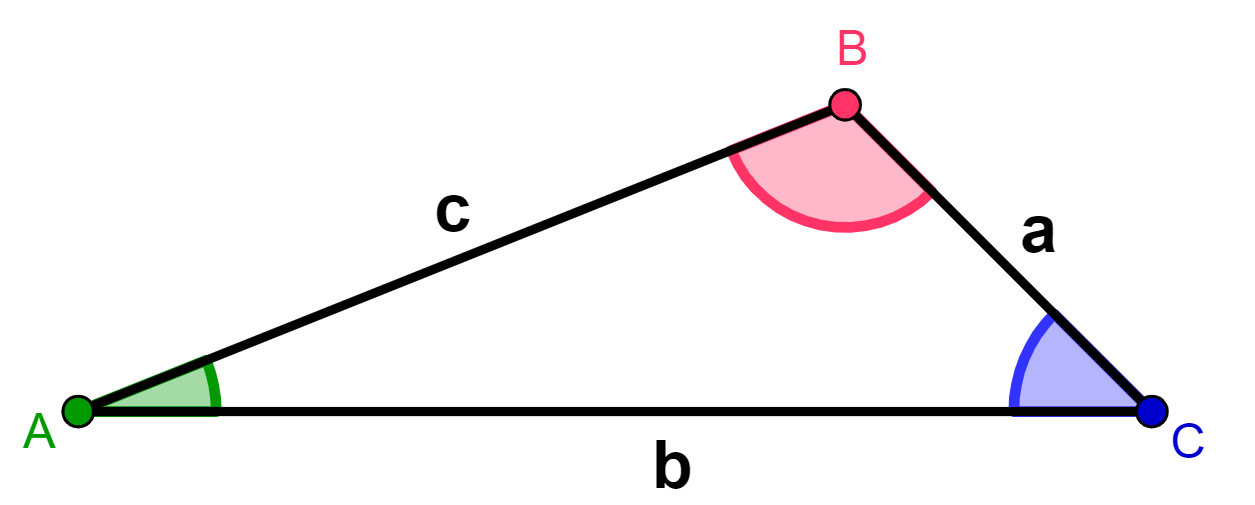
Considere um triângulo ABC qualquer, como o da figura abaixo:

Traçando a altura (h) com relação ao lado AC, podemos observar que o triângulo ABH que se formou é um triângulo retângulo.

Portanto, pelas razões trigonométricas, temos que:

De onde obtemos que a altura h pode ser expressa como:

Substituindo essa expressão encontrada na fórmula da área do triângulo, temos que:

Assim, encontramos uma primeira fórmula para calcular a área do triângulo usando ângulos.

1ª Fórmula

De modo equivalente, podemos ver o triângulo BCH também é triângulo retângulo. Então:

Assim, outra forma de obter a altura h é:

Nesse caso, temos uma segunda fórmula que também pode ser usada para calcular a área do triângulo.

2ª fórmula

Perceba que em cada uma dessas fórmulas utiliza-se o seno do ângulo e a medida dos dois lados adjacentes a ele.

Então, além dessas duas primeiras fórmulas, pode ser demonstrada uma terceira fórmula para calcular a área do triângulo usando ângulos.

3ª fórmula

Para um mesmo triângulo, a área pode ser calculada por qualquer uma dessas três fórmulas, o resultado será o mesmo.

Cabe, então, verificar quais são as medidas de lados e ângulos disponíveis no triângulo e identificar a melhor fórmula a ser utilizada.

Você também pode se interessar:

• Triângulo equilátero
• Triângulo isósceles
• Triângulo escaleno
• Teorema de Pitágoras
• Tabela trigonométrica