Triângulo equilátero
Veja o que são triângulos equiláteros, quais suas principais características e fórmulas para calcular altura, perímetro e área.
Os triângulos são polígonos que possuem três lados e podem ser classificados de acordo com as medidas desses lados.
Quando os três lados do triângulo são de tamanhos iguais, dizemos que eles são congruentes e chamamos o triângulo de triângulo equilátero.
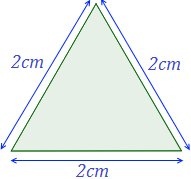
Veja um exemplo de triângulo equilátero, onde os três lados medem 2 cm:
Propriedades do triângulo equilátero
As propriedades dos triângulos equiláteros são características que podem ser observadas em qualquer triângulo com três lados iguais.
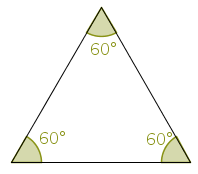
Um triângulo que possui três ângulos menores que 90° é chamado de triângulo acutângulo. Portanto, todo triângulo equilátero é um triângulo acutângulo, já que seus três ângulos medem 60°, que é menor que 90°.
Contudo, o inverso nem sempre é verdadeiro, nem todo triângulo acutângulo é um triângulo equilátero.
Triângulo isósceles é qualquer triângulo que possui pelo menos dois lados de mesma medida.
Assim, triângulos que possuem dois lados iguais e um diferente, assim como triângulos que possuem três lados iguais, são isósceles.
Portanto, todo triângulo equilátero é isósceles, mas nem todo triângulo isósceles é equilátero.
A bissetriz é um segmento de reta que divide um ângulo em dois ângulos de mesma medida e a mediana é um segmento de reta que liga o vértice ao ponto médio do lado oposto.
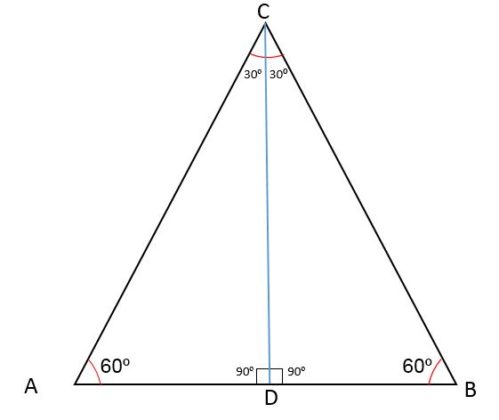
Observe que, ao traçar a altura em um triângulo equilátero, obtemos dois triângulos retângulos.
Altura do triângulo equilátero
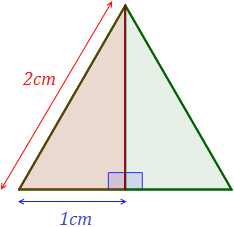
A altura do triângulo equilátero corresponde a um dos lados de um triângulo retângulo. Desse modo, a altura pode ser obtida a partir do teorema de Pitágoras.
A fórmula da altura do triângulo equilátero é:
Em que:
h: altura do triângulo
L: medida do lado do triângulo
Exemplo: Calcule a altura do triângulo equilátero de lado 2 cm.
Substituindo L por 2 na fórmula, temos que:
A altura do triângulo é igual a .
Perímetro do triângulo equilátero
O perímetro de um triângulo qualquer é dado pela soma das medidas dos três lados.
Como em um triângulo equilátero os lados são iguais, podemos calcular o perímetro do triângulo equilátero da seguinte forma:
Em que:
P: perímetro do triângulo
L: medida do lado do triângulo
Exemplo: Calcular o perímetro de um triângulo equilátero de lado igual a 5 cm.
P = 3. 5 = 15
O perímetro do triângulo é igual a 15 cm.
Área do triângulo equilátero
A área do triângulo é dada pela multiplicação da medida da base pela altura dividida por 2.
No caso do triângulo equilátero, já vimos que possui uma fórmula para calcular a altura com base na medida do lado do triângulo.
Com alguns cálculos, é possível mostrar que a fórmula da área do triângulo equilátero, sem precisar da medida da altura, é:
Em que:
A: área do triângulo
L: medida do lado do triângulo
Essa é uma fórmula muito útil, pois observe que, para utilizá-la, basta saber a medida do lado do triângulo equilátero. Isso significa que não precisamos da medida da altura do triângulo para saber sua área.
Você também pode se interessar:
- Relações métricas no triângulo retângulo
- Lista de exercícios sobre a área do triângulo
- Condição da existência de um triângulo
- Lista de exercícios sobre semelhança de triângulos

Os comentários estão fechados, mas trackbacks E pingbacks estão abertos.