Ângulos complementares e suplementares
Alguns ângulos podem ser classificados em complementares ou suplementares. Entenda essa classificação a partir de exemplos simples e veja exercícios resolvidos sobre o assunto.
A medida de um ângulo corresponde à medida de sua abertura, que é expressa em graus (°) e pode variar de 0° a 360°. Alguns ângulos muito utilizados recebem nomes especiais, como ângulo reto e ângulo raso.
- Ângulo reto: é o ângulo de 90°;
- Ângulo raso: é o ângulo de 180°.
Quando dois diferentes ângulos formam, juntos, um ângulo reto, eles são chamados de ângulos complementares e, quando formam, juntos, um ângulo raso, de suplementares.
Vamos entender melhor sobre essas duas classificações?
Ângulos complementares
Temos dois ângulos complementares quando a soma das medidas é igual a 90°, ou seja, quando juntos eles formam um ângulo reto.
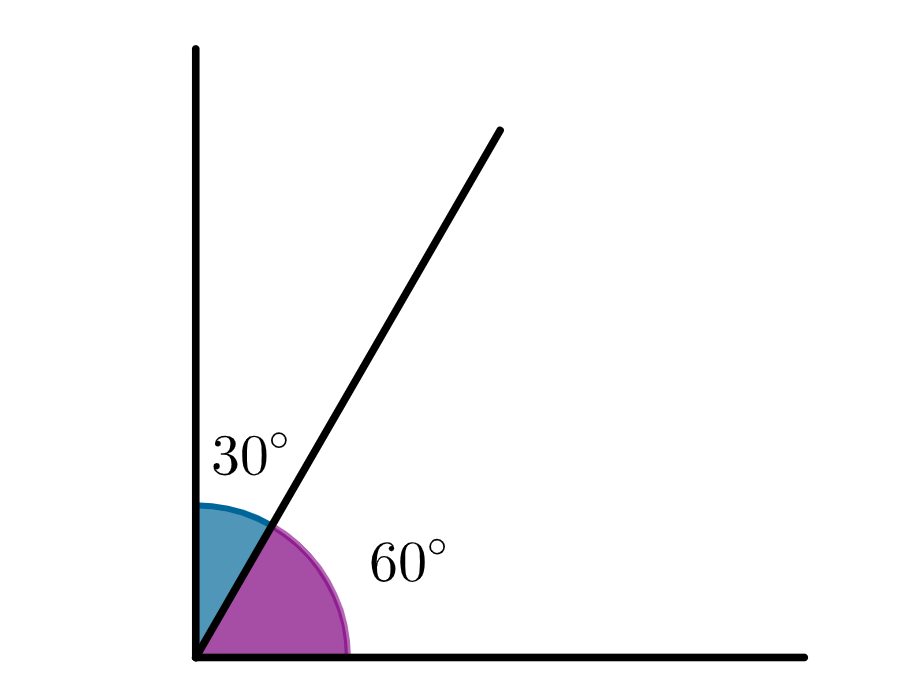
Exemplo: A soma dos ângulos abaixo é 30° + 60° = 90°. Logo, eles são complementares.
Ângulos suplementares
Temos dois ângulos suplementares quando a soma das medidas é igual a 180°, isto é, quando juntos eles formam um ângulo raso.
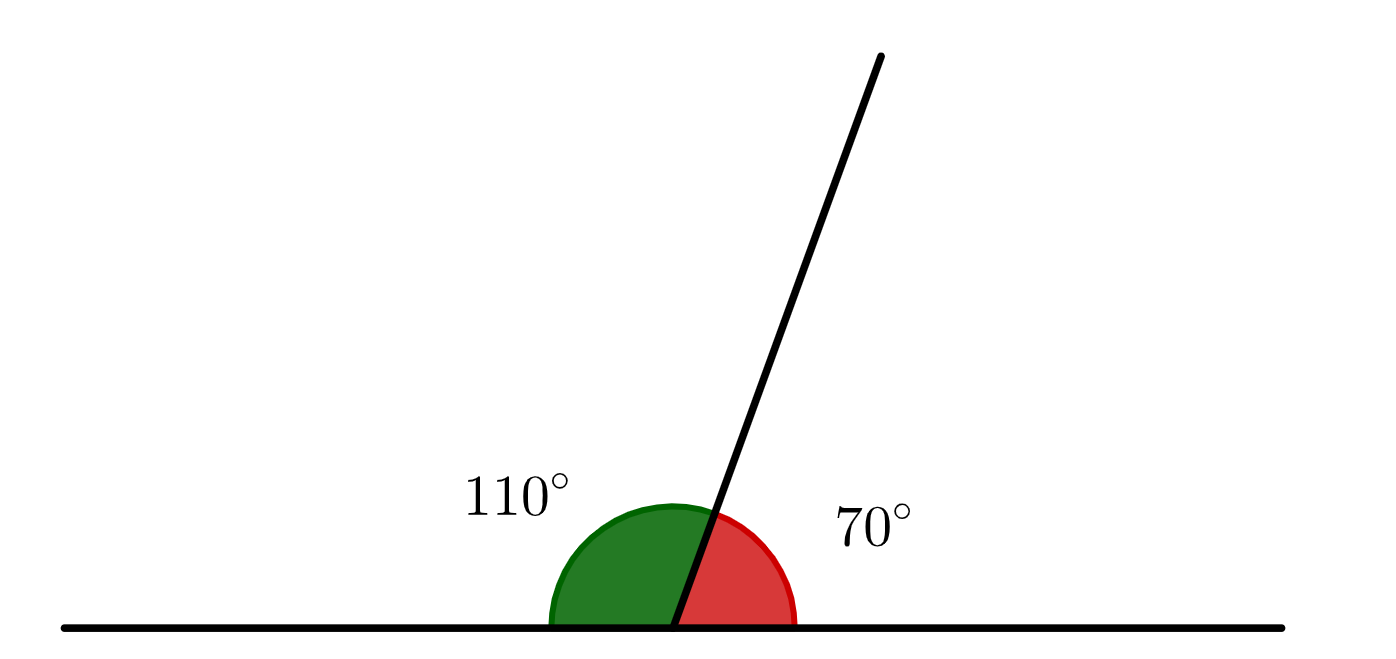
Exemplo: A soma dos ângulos abaixo é 110° + 70° = 180°. Portanto, eles são suplementares.
Exercícios com ângulos complementares e suplementares
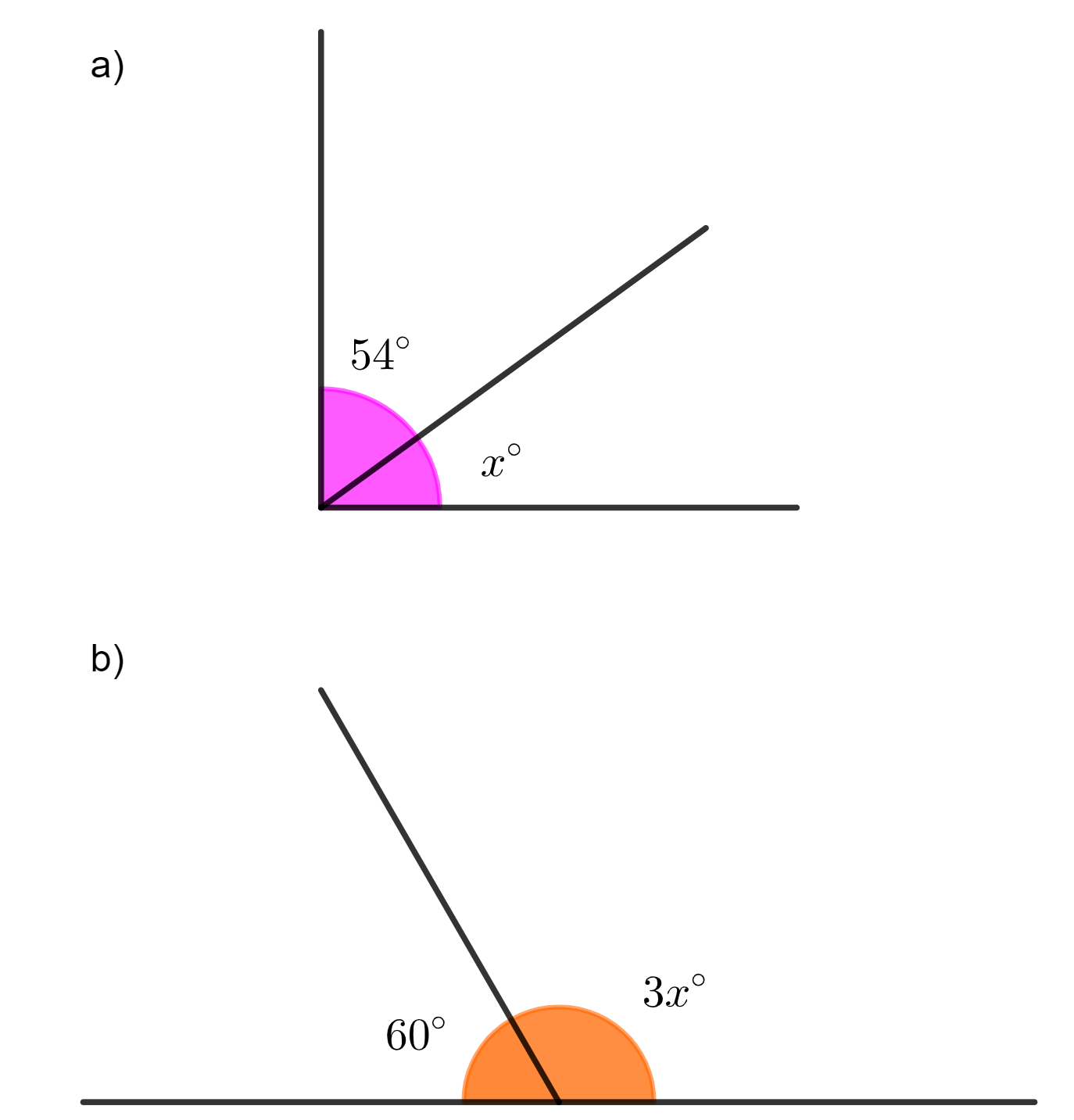
Questão 1. Calcule a medida x nos seguintes casos:
Questão 2. Determine a medida do:
a) complemento do ângulo de 15°.
b) suplemento do ângulo de 15°.
c) complemento do ângulo de 87°.
d) suplemento do ângulo de 87°.
Respostas da questão 1
a) Podemos observar, na imagem, que os ângulos são complementares, pois juntos formam um ângulo reto. Então, a soma dos dois ângulos deve ser igual a 90°, ou seja,
54° + x = 90°
Resolvendo essa equação, encontramos o valor de x:
54° + x = 90°
x = 90° – 54°
x = 36°
b) Nesse item, os ângulos são suplementares, pois formam um ângulo raso. Assim, a soma das medidas deve ser igual a 180°, então:
60° + 3x = 180°
Resolvendo:
60° + 3x = 180°
3x = 180° – 60°
3x = 120°
x = 120°/3
x = 40°
Respostas da questão 2
a) 90° – 15° = 75°
Logo, o complemento do ângulo de 15° é o ângulo de 75°.
b) 180° – 15° = 165°
Assim, o suplemento do ângulo de 15° é o ângulo de 165°.
c) 90° – 87° = 3°
Portanto, o complemento do ângulo de 87° é o ângulo de 3°.
d) 180° – 87° = 93°
Logo, o suplemento do ângulo de 87° é o ângulo de 93°.
Veja também:
- Equação do primeiro grau
- Inequações – Primeiro e segundo grau
- Sistemas de equações
- Áreas de figuras planas
- Teorema de Pitágoras – História, fórmula, Triângulo Pitagórico

Os comentários estão fechados, mas trackbacks E pingbacks estão abertos.