Área do cubo
O cubo é formado por seis faces quadrangulares congruentes. Veja como calcular a área da base, a área lateral e área total dessa figura!
A área do cubo corresponde à medida da sua superfície, sendo dividida em três: área da base, área da lateral e área total.
Antes de ver como calcular cada uma dessas áreas, lembre-se de algumas características importantes do cubo.
O cubo é um sólido geométrico (uma figura espacial) que se classifica como um poliedro por suas faces serem polígonos.
Mais especificamente, o cubo possui 6 faces e todas elas são quadrados congruentes (iguais). Assim, a medida do lado em cada um desses quadrados é a mesma e recebe o nome de aresta do cubo.
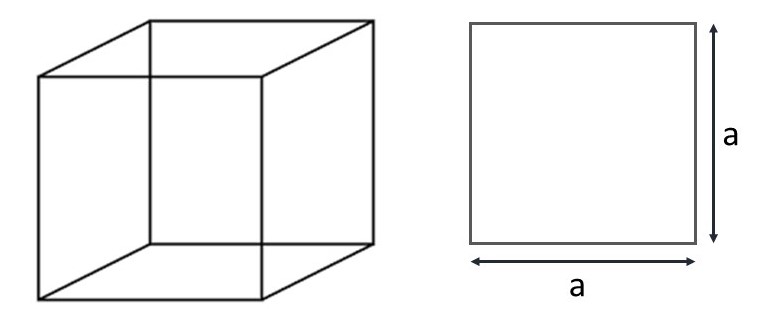
Na figura a seguir, é apresentado um cubo de aresta a, ao lado de uma das suas faces.
Área da base
No cubo, todas as faces são iguais, então qualquer uma delas pode ser base.
Considerando a face voltada para cima ou a face voltada para baixo como base do cubo, a área da base corresponde a área do quadrado de lado a (aresta do cubo).
A fórmula da área da base do cubo é:
Em que:
: área da base;
: aresta do cubo.
Se quisermos a área das duas bases, devemos multiplicar a área da base por 2.
Área lateral
Duas faces opostas do cubo são base e as outras quatro faces restantes são faces laterais. Assim, a área lateral corresponde a quatro vezes a área de um quadrado de lado a (aresta do cubo).
A fórmula da área lateral do cubo é:
Em que:
: área lateral;
: aresta do cubo.
Área total
A área total do cubo é a soma das áreas de todas 6 as faces, ou seja, é a área das duas bases mais a área lateral:
A fórmula da área total do cubo é:
Em que:
: área total;
: aresta do cubo.
Você também pode se interessar:

Os comentários estão fechados, mas trackbacks E pingbacks estão abertos.