Área do quadrado

Muitas superfícies planas têm a forma de um quadrado e para saber o espaço ocupado por elas, é necessário calcular a área. Então, vamos aprender como calcular a área de qualquer quadrado?

Por Elainy Marciano Publicado em 13/02/2020 - 16:02

Quando se fala em Geometria Plana, o quadrado é uma das figuras mais simples e lembradas. No entanto, existem características importantes e muito úteis do quadrado, que são desconhecidas por muitas pessoas. O cálculo da sua área é uma delas.

Quando calculamos a área de um quadrado, obtemos a medida da sua superfície, que é o espaço que ele ocupa. Saber esse espaço é indispensável, por exemplo, em construções civis.

Veja mais

O limite numérico: até onde vai o maior número que conhecemos?

Reditec debate ensino profissional e tecnológico

Então, por que não conhecer um pouco mais sobre o quadrado e aprender como calcular sua área?!

O que é um quadrado?

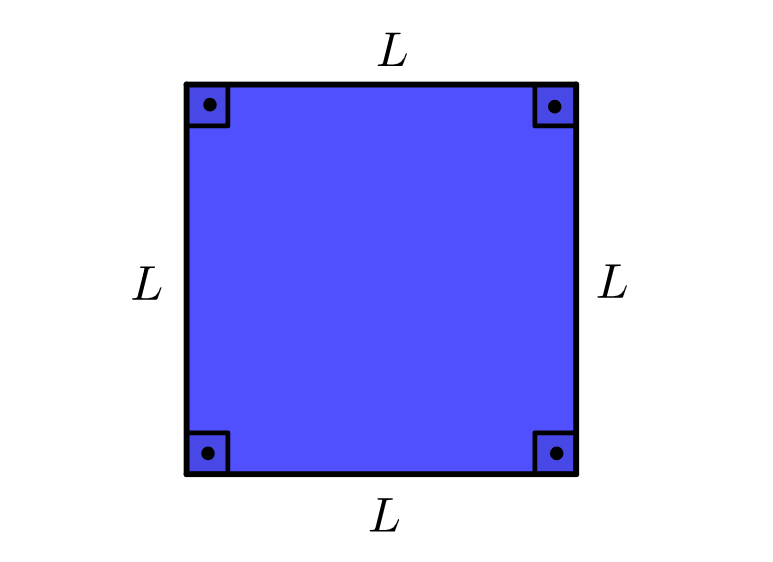
O quadrado é um quadrilátero (ou quadrângulo), pois possui quatro lados (quatro ângulos) e também é um paralelogramo, por ter os lados opostos paralelos.

Todos os lados do quadrado são congruentes, o que significa que todos eles têm a mesma medida.

Além disso, o quadrado também é um retângulo. Isso mesmo, um retângulo! É que os quatro ângulos internos do quadrado são ângulos retos, uma condição necessária e suficiente para ser um retângulo.

Fórmula da área do quadrado

Como em qualquer outro paralelogramo, a área do quadrado é dada pela medida da base multiplicada pela altura: Área do paralelogramo = base x altura.

Como todos os lados do quadrado têm a mesma medida, é convencional chamar cada um deles simplesmente de lado ( $\dpi{120} L$ ).

Então, no quadrado, temos que base x altura = lado x lado. Assim, a fórmula da área de quadrado pode ser expressa da seguinte forma:

$\dpi{120} \acute{A}rea \ do \ quadrado = L \times L$

ou ainda, de forma equivalente,

$\dpi{120} \acute{A}rea \ do \ quadrado = L^2$

Onde $\dpi{120} L$ = medida do lado.

Perímetro do quadrado

O perímetro de um quadrado é dado pela soma de seus quatro lados: L + L + L+ L = 4 L.

Assim, a fórmula para calcular o perímetro de um quadrado pode ser expressa como:

$\dpi{120} Per\acute{\imath}metro \ do \ quadrado = 4L$

Diagonal do quadrado

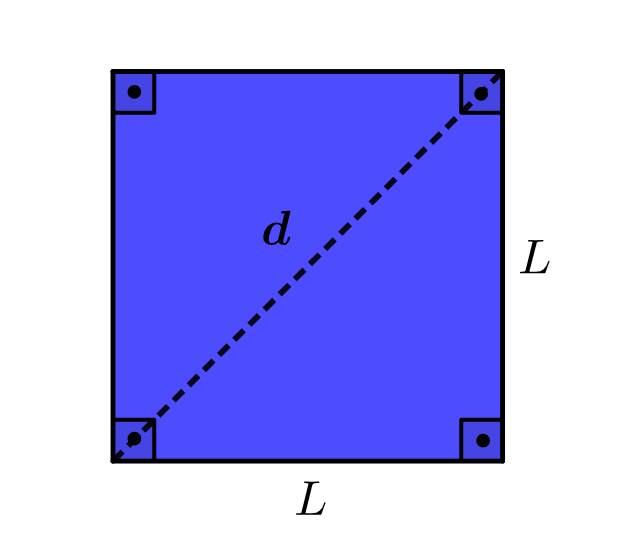
A diagonal (d) de um quadrado o divide em dois triângulos retângulos. Veja:

Assim, para encontrar a medida da diagonal, podemos utilizar o Teorema de Pitágoras, que diz que a hipotenusa ao quadrado equivale a soma dos quadrados dos catetos.

No quadrado, a diagonal é a hipotenusa e os catetos são os lados. Desse modo, temos uma fórmula que relaciona a medida da diagonal com a medidas dos lados (L) do quadrado:

$\dpi{120} d^2 = L^2 + L^2$

Aplicando a raiz quadrada em ambos os lados da equação, obtemos a fórmula para encontrar a diagonal do quadrado:

$\dpi{120} \flushleft \textit{d} = \sqrt{L^2 + L^2}\\ \textit{d} = \sqrt{2L^2} \\ \textit{d} = L\sqrt{2}$

Exemplos

Exemplo 1: Calcular a área, o perímetro e a diagonal do quadrado abaixo:

Área:

$\dpi{120} \flushleft \textit{A} = L^2\\ \textit{A} = (5 m)^2\\ \textit{A} = 25 m^2$

Perímetro:

$\dpi{120} \flushleft \textit{P} = 4L\\ \textit{P}= 4 \cdot \ 5 \ \textnormal{m}\\ \textit{P} = 20 m$

Diagonal:

$\dpi{120} \flushleft \textit{d }= L \cdot \sqrt{2}\\ \textit{d} = 5 m\cdot \sqrt{2}\\ \textit{d} \approx 7,07 \ \textnormal{m}$

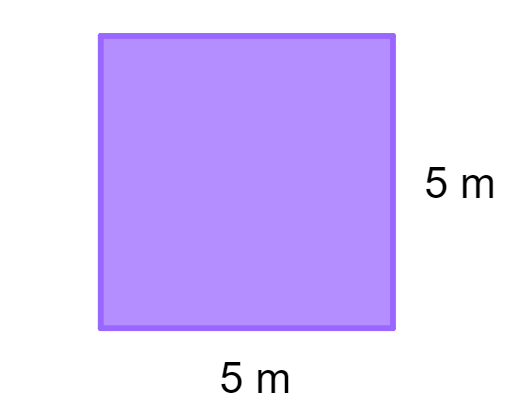
Então, esse quadrado tem 25 m² de área, 20 m de perímetro e a medida da diagonal é aproximadamente 7,07 m.

Exemplo 2: Calcular o perímetro e a diagonal de um quadrado com 144 cm² de área.

Para calcular o perímetro e a digonal precisamos da medida do lado do quadrado. Para descobrir esse valor, vamos utilizar a informação da área que foi dada.

A área de qualquer quadrado é igual $\dpi{120} L^2$ . Se nesse quadrado, a área é igual a 144 cm², então, podemos dizer que:

$\dpi{120} L^2 = 144 \ \textnormal{cm}^2$

Aplicando a raiz quadrada, temos que:

$\dpi{120} \flushleft \textit{L} = \sqrt{144 \ \textnormal{cm}^2} \\ \textit{L} = 12 cm$

Agora já podemos calcular o perímetro e a diagonal:

Perímetro:

$\dpi{120} \flushleft \textit{P} = 4L\\ \textit{P}= 4 \cdot \ 12 \ \textnormal{cm}\\ \textit{P} = 48 cm$

Diagonal:

$\dpi{120} \flushleft \textit{d }= L \cdot \sqrt{2}\\ \textit{d} = 12 cm\cdot \sqrt{2}\\ \textit{d} \approx 16,97 \ \textnormal{cm}$

Logo, o quadrado tem 48 cm de perímetro e diagonal em torno de 16,97 cm.

Você também pode se interessar: