Baricentro de um triângulo

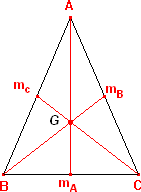
O baricentro de um triângulo é o ponto de encontro entre as suas três medianas. Na figura abaixo, o baricentro é o ponto G.

Medianas do triângulo

Os triângulos são polígonos de três lados, que podem ser classificados de acordo com as medidas dos lados ou de acordo com as medidas dos ângulos internos.

Contudo, independente do tipo, qualquer triângulo possui sempre três medianas.

Cada umas das medianas do triângulo é um segmento de reta que liga um vértice ao ponto médio do lado oposto a ele.

O ponto médio de um segmento é o ponto que está exatamente na metade do segmento.

Coordenadas do baricentro do triângulo

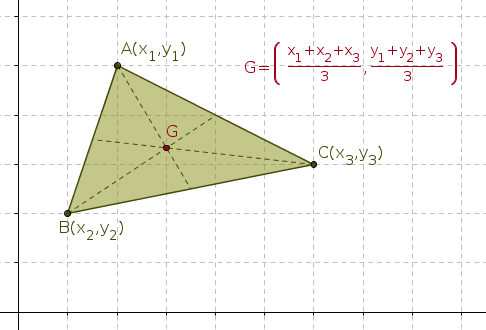
Para encontrar as coordenadas do baricentro do triângulo, utilizam-se as coordenadas dos vértices do triângulo no plano cartesiano.

A abscissa do baricentro é dada pela média das abscissas dos vértices e a ordenada do baricentro é dada pela média das ordenadas dos vértices.

Desse modo, sendo , , , os vértices do triângulo e o baricentro , temos:

e

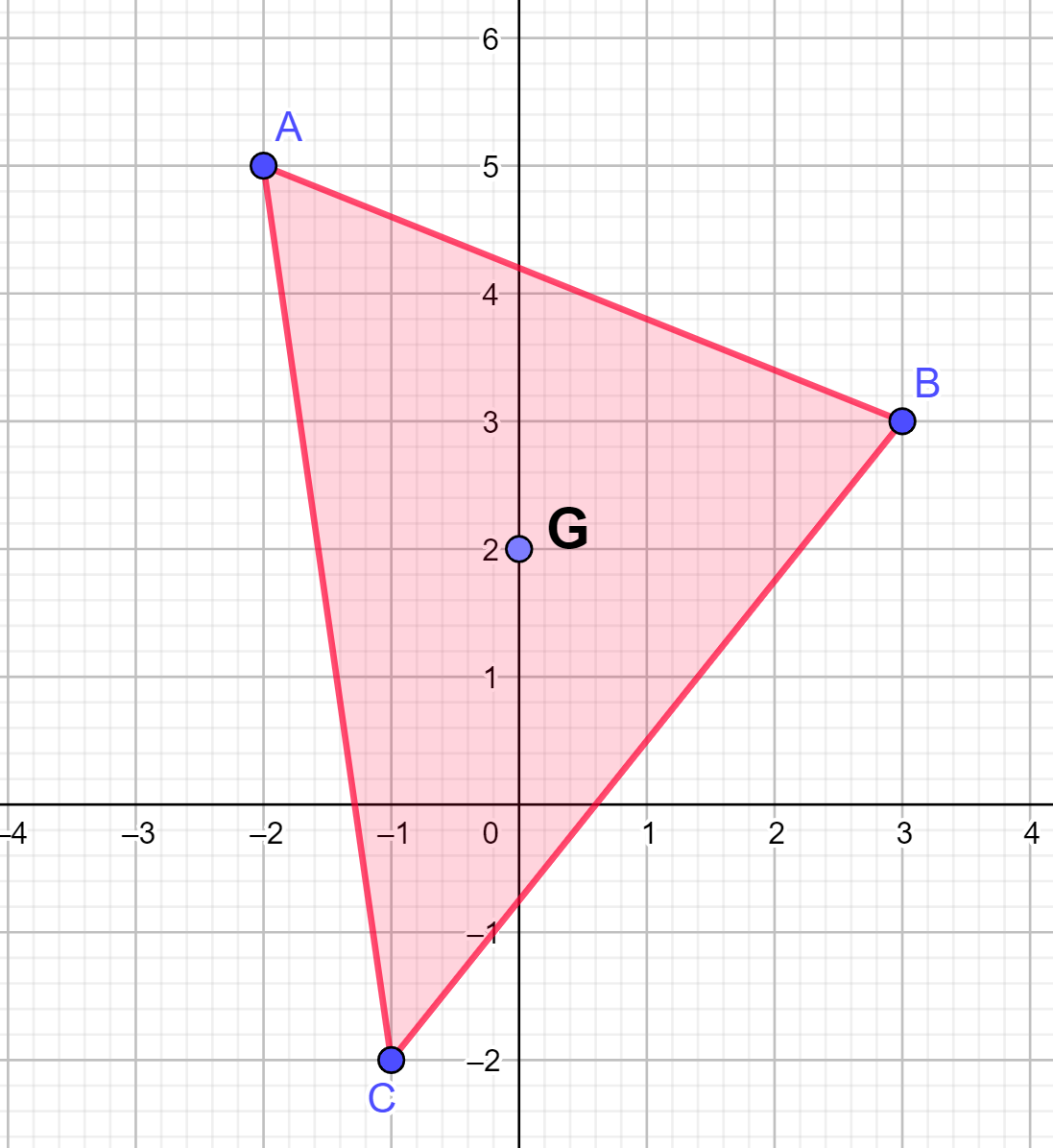
Exemplo: Determine as coordenadas do baricentro de um triângulo de vértices A(-2, 5), B(3, 3) e C(-1, -2).

Substituindo as coordenadas dos vértices nas fórmulas apresentadas, temos que:

Portanto, o baricentro é o ponto G(0, 2).

Você também pode se interessar:

• Bissetriz
• Mediatriz
• Triângulo isósceles
• Triângulo escaleno
• Triângulo equilátero