Congruência de triângulos

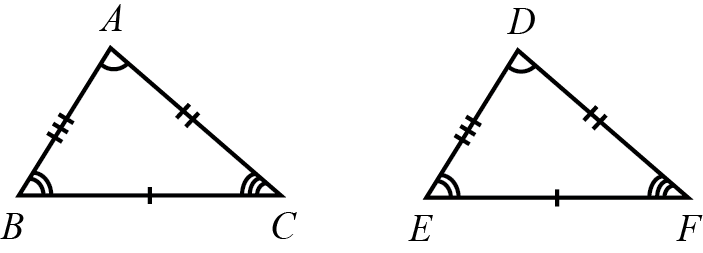
Em geometria, a palavra congruência está relacionada a tamanhos ou medidas iguais. Assim, dois triângulos são congruentes quando possuem lados e ângulos, respectivos, de mesma medida.

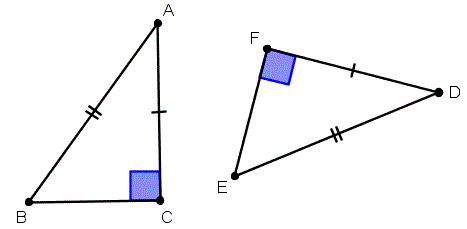
Os triângulos ABC e DEF abaixo são congruentes, veja:

Cada lado do triângulo ABC é do mesmo tamanho do respectivo lado no triângulo DEF, e cada ângulo do triângulo ABC tem a mesma medida do respectivo ângulo no triângulo DEF.

Lados:

• AB ≅ DE
• BC ≅ EF
• AC ≅ DF

Ângulos:

• A ≅ D
• B ≅ E
• C ≅ F

Então, você pode estar pensando que para verificar a congruência entre dois triângulos, teremos sempre que verificar a congruência entre seis elementos (3 ângulos e 3 lados), certo?

Saiba que nem sempre, pois existem algumas condições que, se forem satisfeitas, são suficientes para que possamos dizer que dois triângulos são congruentes.

Essas condições podem ser especificadas em 4 casos principais. Vamos ver quais são?

 Casos de congruência de triângulos

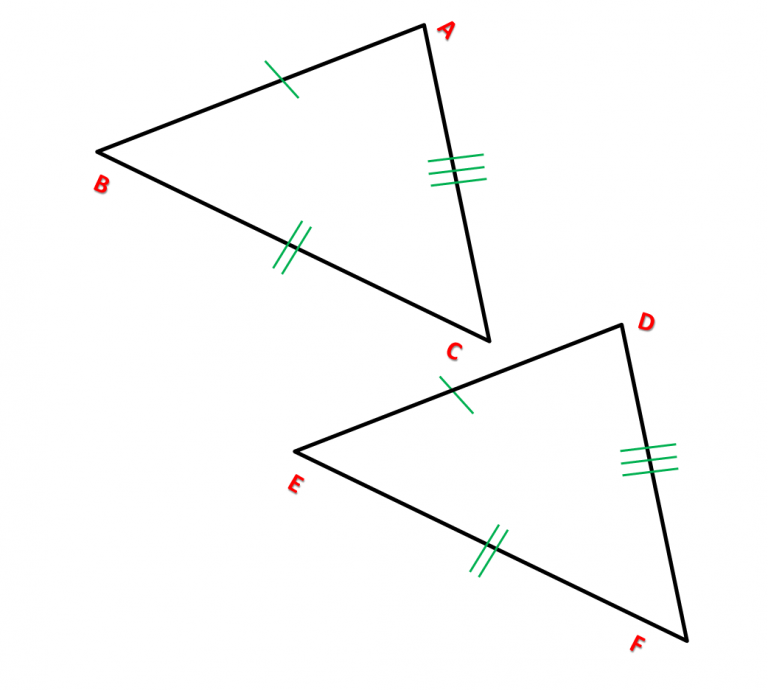
Caso 1: Lado, Lado, Lado (LLL).

Em outras palavras, se dois triângulos têm lados de mesma medida, então, eles automaticamente também vão ter ângulos de mesma medida, e não precisamos verificar isso para dizer que são congruentes.

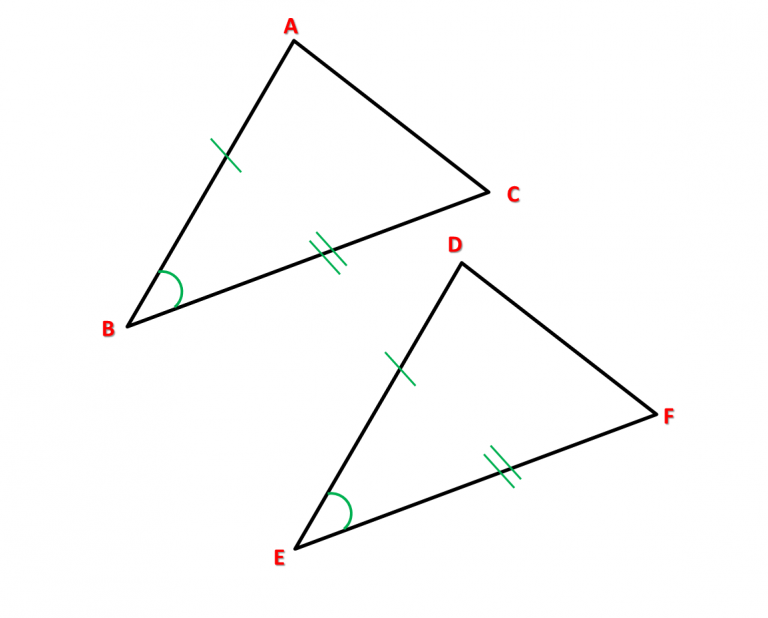
Caso 2: Lado, Ângulo, Lado (LAL).

Isso significa que, satisfeitas essas condições, o terceiro lado e os outros dois ângulos dos triângulos também serão congruentes, mas não precisaremos verificar isso.

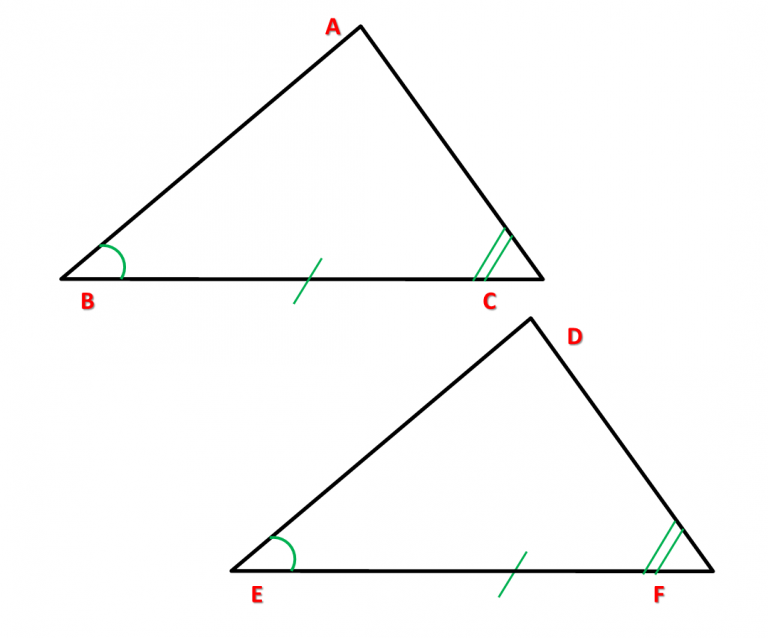
Caso 3: Ângulo, Lado, Ângulo (ALA).

Assim, podemos dizer que dois triângulos que satisfazem essas condições também terão o terceiro ângulo e os outros dois lados congruentes.

Caso 4: Lado, Ângulo adjacente, Ângulo oposto (LAAo).

Aqui, também podemos dizer, que os outros dois lados e o terceiro ângulo também são congruentes se essas condições são satisfeitas.

Congruência de triângulos retângulos

Um caso especial de congruência de triângulos, é a congruência entre triângulos retângulos, que são aqueles que possuem um ângulo reto (90° graus).

Lembre-se: a hipotenusa é o lado oposto ao ângulo de 90° e os catetos são os outros dois lados do triângulo.

Você também pode se interessar:

• Área do Triângulo
• Condição da existência de um triângulo
• Teorema de Pitágoras – História, fórmula, Triângulo Pitagórico
• Trigonometria no Triângulo Retângulo