Coordenadas do vértice da parábola

Quando marcamos vários pares ordenados de uma função do 2° grau, o gráfico que obtemos corresponde a uma parábola. O vértice nada mais é do que é um ponto da função no qual ela muda o sentido.

Desse modo, o vértice está associado a concavidade da parábola, podendo ser o ponto de mínimo ou o ponto de máximo:

• Quando a parábola é côncava para cima, então o vértice é o ponto de mínimo da função.
• Quando a parábola é côncava para baixo, então o vértice é o ponto de máximo da função.

Se o vértice é um ponto da parábola, então, ele possui coordenadas. Mas quais são as coordenadas do vértice? Existe uma fórmula para encontrar essas coordenadas?

Sim. Existem algumas formas de encontrar as coordenadas do vértice de uma parábola. As seguir, vamos mostrar uma delas.

Como calcular as coordenadas do vértice da parábola

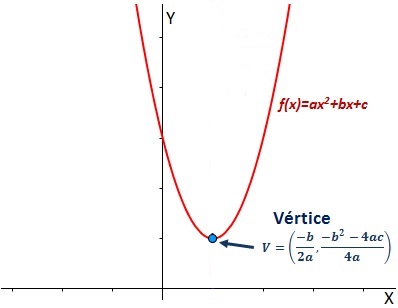
Considerando uma função do 2° grau, , o vértice da parábola é um ponto , com coordenadas dadas por:

 Em que  é chamado de discriminante e corresponde àquele mesmo valor que calculamos para aplicar na fórmula de Bhaskara e encontrar as raízes de uma equação do 2° grau.

Exemplo: Determine o vértice da função f(x) = x² + 3x – 28.

Nessa função, temos a = 1, b= 3 e c = -28.

Aplicando esses valores nas fórmulas, temos:

e

.

Portanto, o vértice da função é o ponto V(-1,5; -30,25).

Você também pode se interessar:

• Exercícios de função do primeiro grau (função afim)
• Função injetora
• Domínio, contradomínio e imagem