Calculando a diagonal do quadrado e do retângulo

Veja como usar o teorema de Pitágoras para calcular a diagonal do quadrado e do retângulo.

Por Elainy Marciano Publicado em 22/09/2020 - 19:29

O quadrado e o retângulo são duas figuras geométricas planas muito comuns no dia a dia e aparecem em diversos problemas matemáticos.

Eles são polígonos de quatro lados, sendo classificados como quadriláteros. Ambos possuem quatro vértices e quatro ângulos internos retos, ou seja, ângulos de 90°.

Veja mais

O limite numérico: até onde vai o maior número que conhecemos?

Reditec debate ensino profissional e tecnológico

Nessas figuras, podemos ligar os vértices não consecutivos, obtendo segmentos de retas chamados de diagonais.

Diagonal do quadrado e do retângulo

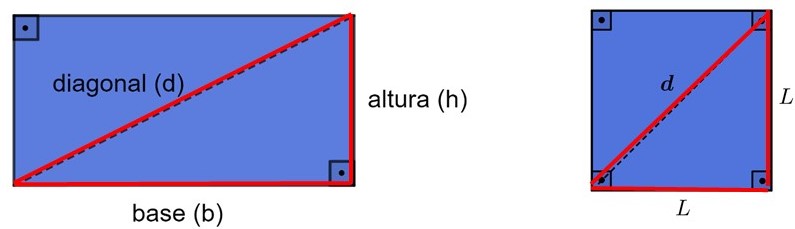
As diagonais do quadrado e do retângulo dividem cada uma das figuras em dois triângulos.

Esses triângulos formados, sempre vão possuir um ângulo reto, portanto, são classificados como triângulos retângulos.

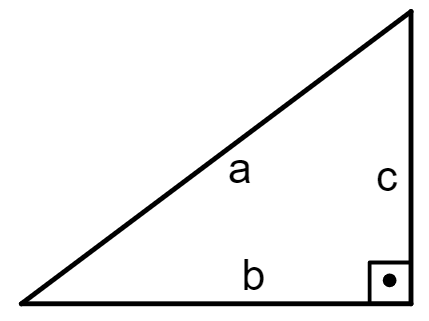
Triângulo Retângulo — Triângulo retângulo

Os triângulos retângulos possuem uma relação muito importante entre as medidas dos seus três lados, conhecida como Teorema de Pitágoras.

Por esse teorema, o quadrado da hipotenusa do triângulo (lado oposto ao ângulo reto) é igual à soma dos quadrados dos catetos do triângulo:

$\dpi{120} \mathrm{a^2 = b^2 + c^2}$

Ou ainda, de forma equivalente: $\dpi{120} \mathbf{a = \sqrt{b^2+c^2}}$

a: hipotenusa
b e c: catetos

Agora, veja que no quadrado e no retângulo, a diagonal corresponde a hipotenusa do triângulo formado e os outros dois lados da figura são os catetos.

Dessa forma, podemos utilizar o teorema de Pitágoras para calcular a diagonal do quadrado e do retângulo.

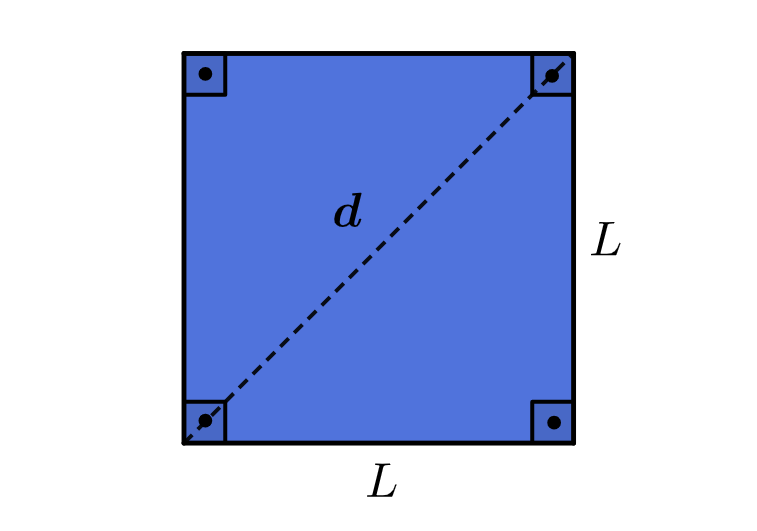
Diagonal do quadrado

$\dpi{120} \mathbf{d = \sqrt{L^2+L^2}}$

Em que L é a medida do lado do quadrado.

Observe, ainda, que essa fórmula pode ser simplificada: $\dpi{120} \mathrm{d = \sqrt{L^2+L^2}= \sqrt{2L^2} = L\sqrt{2}}$ .

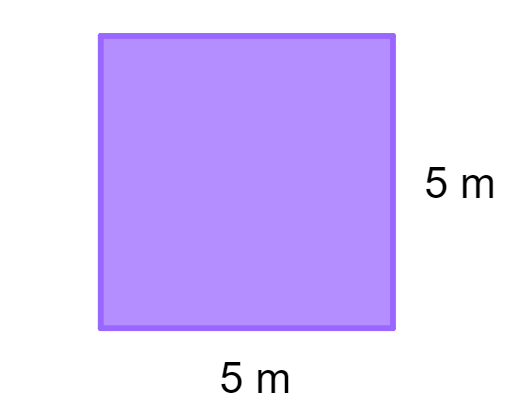
Exemplo: Calcular a medida da diagonal de um quadrado cujos lados medem 5 metros cada.

Temos L = 5. Vamos aplicar esse valor na fórmula da diagonal do quadrado:

$\dpi{120} \mathbf{d = \sqrt{5^2+5^2}}$

$\dpi{120} \mathbf{d = \sqrt{50}}$

$\dpi{120} \mathbf{d = 5\sqrt{2}}$

Portanto, a diagonal desse quadrado mede $\dpi{120} 5\sqrt{2}$ metros, o que é aproximadamente igual a 7,07 metros.

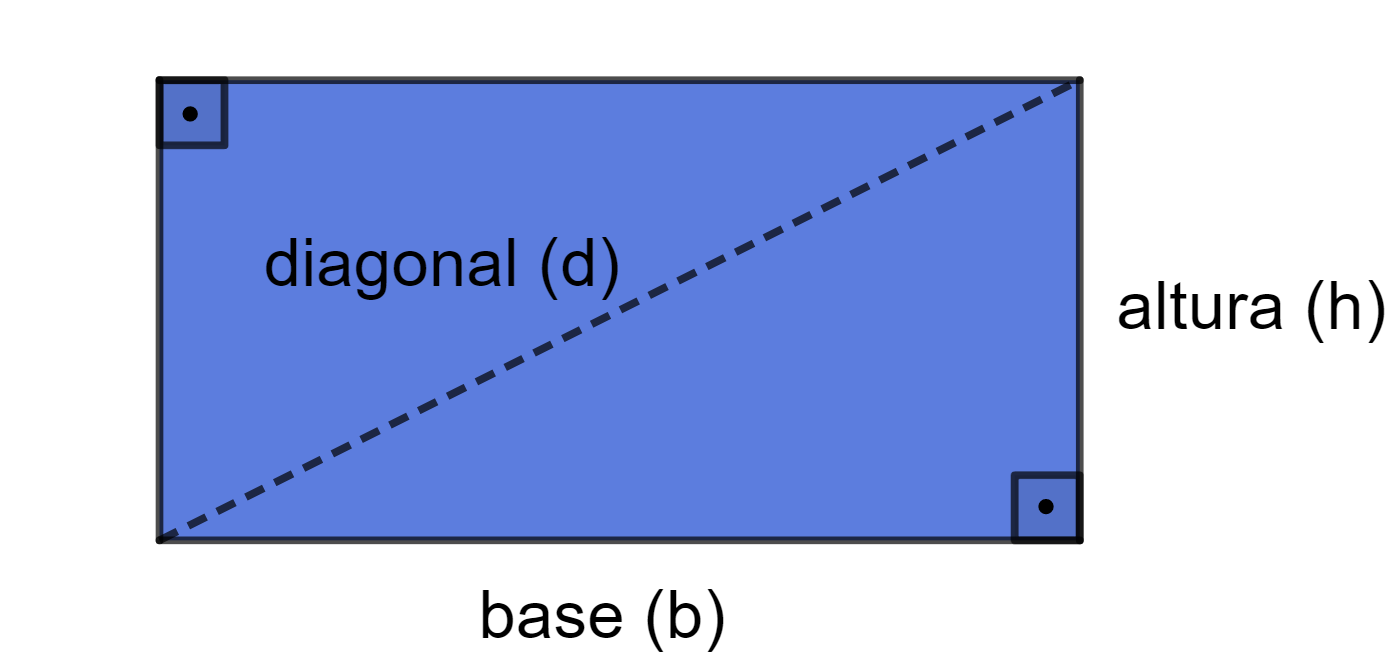
Diagonal do retângulo

$\dpi{120} \mathbf{d = \sqrt{b^2+h^2}}$

Em que b é a medida da base e h é a altura do retângulo.

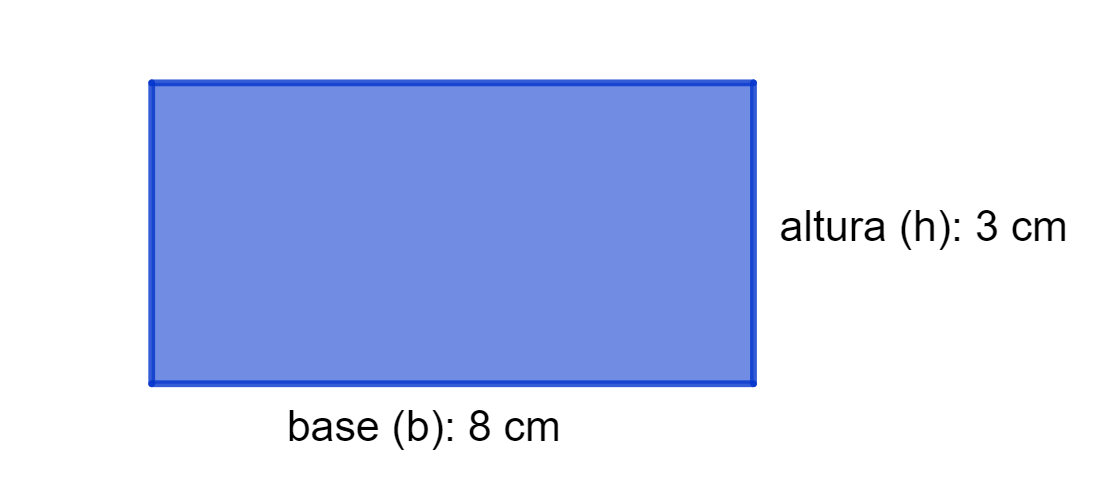
Exemplo: Calcular a medida da diagonal de um retângulo cuja base mede 8 cm e a altura é igual 3 cm.

Temos b = 8 e h = 3. Vamos aplicar esses valores na fórmula da diagonal do retângulo:

$\dpi{120} \mathbf{d = \sqrt{8^2+3^2}}$

$\dpi{120} \mathbf{d = \sqrt{64+9}}$

$\dpi{120} \mathbf{d = \sqrt{73}}$

Portanto, a diagonal desse retângulo mede $\dpi{120} \sqrt{73}$ centímetros, que é aproximadamente igual a 8,54 centímetros.

Você também pode se interessar:

Diagonal Teorema de Pitágoras