Dispositivo prático de Briot-Ruffini
Existem alguns métodos de calcular a divisão entre polinômios, o dispositivo de Briot-Ruffini é uma deles. Veja como funciona!
O dispositivo prático de Briot-Ruffini é um método para efetuar a divisão de um polinômio por um binômio do 1º grau.
Considere um polinômio de grau n:
E um binômio da forma:
ou
Para utilizar o dispositivo de Briot-Ruffini e calcular a divisão de por
, precisamos dos coeficientes
de
e da raiz de
, que é determinada resolvendo a equação
.
Como funciona o dispositivo de Briot-Ruffini
Vamos mostrar como calcular a divisão de um polinômio por um binômio usando o dispositivo de Biot-Ruffini, a partir de um exemplo.
Exemplo:
Vamos dividir o polinômio por
.
Como temos um polinômio de grau 3, devemos ter os coeficientes . Como o termo
não aparece no polinômio, o coeficiente
é igual a 0.
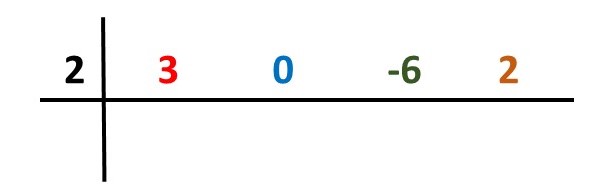
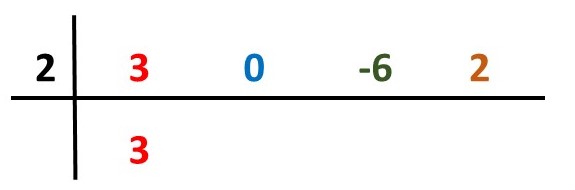
Os coeficientes são 3, 0, -6 e 2.
- Resto: 14
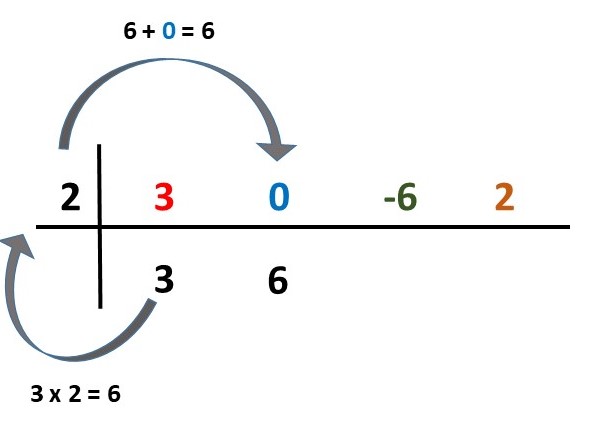
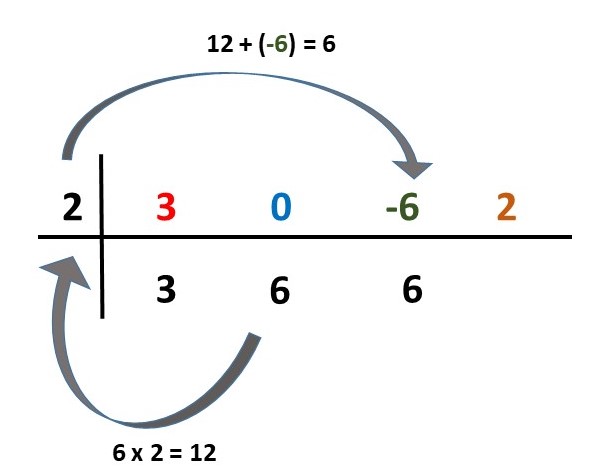
- Coeficientes: 3, 6 e 6.
Dividimos um polinômio de grau 3, então, polinômio obtido será de grau 2.
Isso significa que .
Você também pode se interessar:
- Divisão de polinômios – Método da chave
- Multiplicação de polinômios
- Adição e subtração de polinômios
- Fatoração de polinômios
- Função polinomial


Os comentários estão fechados, mas trackbacks E pingbacks estão abertos.