Polinômios

Um polinômio é uma adição algébrica de termos que podem ser números, variáveis ou a multiplicação entre números e variáveis.

Exemplos de polinômios:

• 5x → polinômio de um termo só
• 3x² + 2y → polinômio de dois termos
• 10ab – 4b + 8 → polinômio de três termos
• x³ – 4y² + z – 5 → polinômio de quatro termos

Grau dos polinômios

Em um polinômio, os termos com uma ou mais variáveis possuem um grau, que é dado pela soma dos expoentes das variáveis. O grau do polinômio é o grau do termo de maior grau.

Exemplos:

x² – 2x + 4 é um polinômio de grau 2, pois:

• x² → grau 2
• 2x → grau 1 (lembre-se que x = x¹)

O maior grau é 2! Então, esse é o grau do polinômio.

a³x² – 2a³x³ + 9ax é um polinômio de grau 6, pois:

• a³x² → como 3 + 2 = 5 → grau 5
• – 2a³x³ → como 3 + 3 = 6 → grau 6
• 9ax → como 1 + 1 = 2 → grau 2

O maior grau é 6! Então, esse é o grau do polinômio.

Monômio, binômino e trinômio

Alguns polinômios recebem nomes especiais de acordo com a quantidade de termos que possuem.

Monômios: são os polinômios que possuem um único termo.

Exemplos:

• 4x
• -xy
• a²bc

Binômios: são polinômios que possuem dois termos.

Exemplos:

• 8x + 2y
• 3a – b
• xy + 2y²

Trinômios: são polinômios que possuem três termos.

Exemplos:

• x² – xy + y²
• y² – 6x +1
• a – 2ab + b²

Operações com polinômios

Vamos ver como realizar as quatro operações básicas entre polinômios.

Adição de polinômios

Na adição de polinômios, basta somar os coeficientes dos termos semelhantes: x com x, xy com xy, a² com a², e assim por diante.

Exemplo:

Soma entre x² – 7x + 10 e 2x² + 9x – 15.

(x² – 7x + 10) + (2x² + 9x – 15) =

x² – 7x + 10 + 2x² + 9x – 15 =

3x² + 2x -5

Termos semelhantes que somamos:

x² + 2x² = 3x²

-7x + 9x = 2x

10 – 15 = -5

Subtração de polinômios

Na subtração de polinômios, basta subtrair os coeficientes dos termos semelhantes: x com x, xy com xy, a² com a², e assim por diante.

Exemplo:

Subtração entre 2x + 5y e x + 3y.

(2x + 5y) – (x + 3y) =

2x + 5y – x – 3y =

x + 2y

Termos semelhantes que subtraímos:

2x – x = x

5y – 3y = 2y

Multiplicação de polinômios

Na multiplicação entre polinômios, temos que multiplicar cada termo do primeiro polinômio por cada um dos termos do segundo polinômio.

Devemos nos lembrar da seguinte propriedade de potenciação:

Na multiplicação de bases iguais, soma-se o expoente e conserva-se a base. Por exemplo, a². a = a³.

Exemplo:

Multiplicar x + 2 por x² – x – 2

(x + 2).(x² – x – 2) =

x . x² – x . x – x . 2 + 2 . x² – 2 . x – 2 . 2 =

x³ – x² – 2x + 2x² – 2x – 4 =

x³ – x² +2x² – 2x – 2x – 4 =

x³ +x² – 4x – 4

Divisão de polinômios

Na divisão de polinômios, o procedimento é semelhante ao da divisão entre dois números, usando o método da chave. Mas aqui, devemos nos lembrar da propriedade de potenciação para a divisão de bases iguais:

Na divisão de potências de bases iguais, conserva-se a base e subtrai-se os expoentes. Por exemplo, a³ : a = a².

Exemplo:

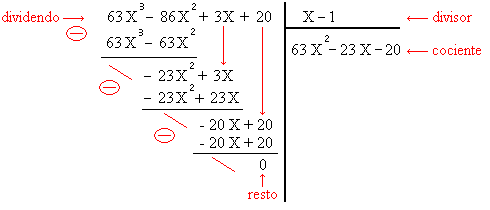
Dividir 63x³ – 86x² + 3x + 20 por x – 1.

1. A primeira coisa a se fazer é dividir 63x³ por x → 63x³ : x = 63x².
2. Colocamos esse valor no quociente e multiplicamos pelo divisor → 63x² . (x -1) = 63x³ – 63x².
3. Então, escrevemos esse resultado embaixo do dividendo e subtraímos.
4. Após isso, repetimos o procedimento da conta de divisão, até obtermos o resto.

Observe que, como o resto é zero, temos dividendo = divisor . quociente, ou seja:

63x³ – 86x² + 3x + 20 = (x – 1) . (63x² – 23x – 20)

Fatoração de polinômios

Para fazer a fatoração de um polinômio, podemos utilizar algumas técnicas. O objetivo é sempre escrever o polinômio como uma multiplicação de polinômios.

Exemplos:

a²x + abx

Podemos fatorar colocando o fator comum em evidência:

a²x + abx = ax . (a + b) → o fator comum é ax.

ax – x + ab – b

Podemos fatorar fazendo o agrupamento:

ax – x + ab – b = x.(a – 1) + b.(a – 1) = (a – 1).(x + b)

Além disso, podemos fazer fatoração utilizando os produtos notáveis.

Você também pode se interessar:

• Lista de exercícios de fatoração
• Equação do primeiro grau
• Inequações – Primeiro e segundo grau
• Escalonamento de matrizes – Resolver sistemas lineares