Exercícios sobre distância entre dois pontos
Confira uma lista de exercícios resolvidos sobre cálculo da distância entre dois pontos.
Quando calculamos a distância entre dois pontos, o que estamos calculando é o tamanho de um segmento de reta que liga os dois pontos e que corresponde à hipotenusa de um triângulo retângulo.
Assim, a fórmula da distância entre dois pontos deriva do Teorema de Pitágoras e é dada por:
A seguir, temos uma lista de exercícios resolvidos sobre distância entre dois pontos.
Lista de exercícios sobre distância entre dois pontos
Questão 1. Calcule a distância entre os pontos (-5, 3) e (4, 3).
Questão 2. Calcule a distância entre os pontos (-2, 5) e (-2, 1).
Questão 3. Calcule a distância entre os pontos (0,-4) e (1, 1) .
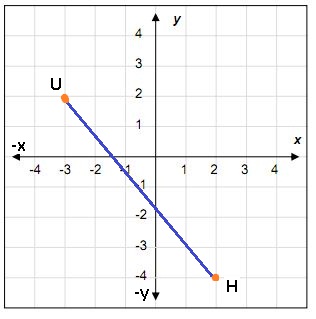
Questão 4. Calcule a distância entre os pontos H e U na figura abaixo.
Questão 5. A distância entre os pontos (2, 3) e (5, y) é igual a 5. Determine os possíveis valores de y.
Questão 6. Encontre um ponto da reta 4x – 8y + 7 = 0 que equidista dos pontos A(1, – 3) e B(2, 1).
Questão 7. Um dos extremos de um segmento de reta que mede 17 unidades é o ponto A(1, -11). Sabendo que a ordenada do outro extremo é 4, encontre sua abscissa.
Resolução da questão 1
Temos os pontos (-5, 3) e (4, 3). Observe que o valor de y é o mesmo nos dois. Assim, trata-se de uma distância horizontal, que pode ser obtida subtraindo os valores de x e aplicando o módulo:
|4 – (-5)| = |9| = 9
Assim, como podemos aplicar a fórmula e encontrar o mesmo resultado:
Resolução da questão 2
Temos os pontos (-2, 5) e (-2, 1). Veja que o valor de x é o mesmo nos dois. Desse modo, trata-se de uma distância vertical, que pode ser obtida subtraindo os valores de y e aplicando o módulo:
|1 – 5| = |-4| = 4
Assim, como podemos aplicar a fórmula e encontrar o mesmo resultado:
Resolução da questão 3
Para determinar a distância entre os pontos (0,-4) e (1, 1), vamos aplicar a fórmula da distância entre dois pontos:
Resolução da questão 4
Observando a figura, podemos ver que os pontos são H(2, -4) e U (-3, 2). Vamos aplicar a fórmula da distância:
Resolução da questão 5
Temos d = 5 e os pontos (2, 3)e (5, y). Então, pela fórmula da distância, temos:
Temos uma equação do 2° grau, que pode ser resolvida através da fórmula de Bhaskara.
Cálculo de delta:
Cálculo de y:
Portanto, os possíveis valores de y são -1 e 7.
Resolução da questão 6
Considere que P(x, y) é o ponto da reta que queremos encontrar.
Utilizando a fórmula da distância, temos que a distância do ponto P ao ponto A é:
E a distância do ponto P ao ponto B é:
Dizer que o ponto P equidista dos pontos, significa dizer que a distância de P até o ponto A é igual a distância de P até o ponto B. Assim, temos que:
Chegamos na equação de uma reta : -2x – 8y -5 = 0. Isso significa que o ponto P(x, y) além de pertencer à reta 4x – 8y + 7 = 0, também deve pertencer à reta -2x – 8y -5 = 0.
Assim, devemos encontrar os valores de x e y que satisfaçam essas duas equações ao mesmo tempo, isto é, temos que resolver um sistema de duas equações.
Multiplicando a segunda equação por (-1), temos que:
Somando as duas equações:
6x + 0 + 12 = 0
6x = -12
x = -12/6
x = -2
Substituindo o valor de x por -2 na 1° equação, temos que:
4x – 8y + 7 = 0
4.(-2) – 8y + 7 = 0
-8 -8y + 7 = 0
-8y = 1
y = -1/8
Portanto, o ponto as coordenadas do ponto são P(-2, -1/8).
Resolução da questão 7
Temos um segmento de reta de tamanho d = 17 com extremos nos pontos A(1, -11) e B(x, 4), onde x corresponde à abscissa que queremos encontrar.
Então, basta aplicar esses valores na fórmula da distância entre dois pontos.
Temos uma equação do 2° grau, que pode ser resolvida através da fórmula de Bhaskara.
Cálculo de delta:
Cálculo de x:
Assim, existem dois possíveis valores para a abscissa x, pode ser -7 ou 9.
Você também pode se interessar:
- Lista de exercícios de polígonos
- Exercícios sobre Teorema de Pitágoras
- Plano cartesiano – O que é, como construir um, como fazer o produto cartesiano

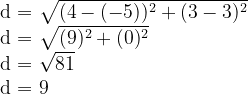
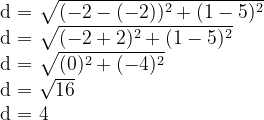
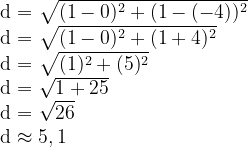
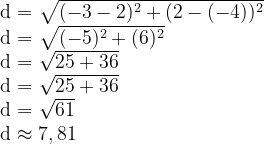
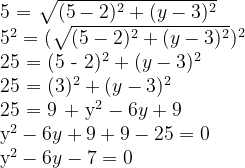
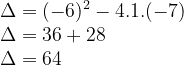
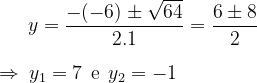
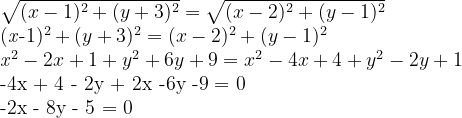
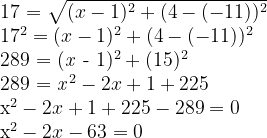
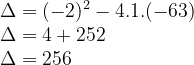
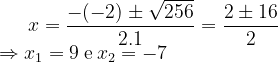
Os comentários estão fechados, mas trackbacks E pingbacks estão abertos.