Lista de exercícios sobre a área do triângulo

Aprenda mais sobre o cálculo da área de um triângulo, a partir de uma lista de exercícios resolvidos sobre esse assunto!

Por Elainy Marciano Publicado em 24/06/2020 - 16:06

A área do triângulo pode ser calculada multiplicando-se a medida da altura pela medida da base e dividindo esse resultado por 2.

O cálculo é simples, mas nem sempre todas as medidas são conhecidas, sendo necessário alguns outros conhecimentos.

Veja mais

O limite numérico: até onde vai o maior número que conhecemos?

Reditec debate ensino profissional e tecnológico

Para saber mais sobre esse assunto, confira uma lista de exercícios resolvidos sobre área de triângulos.

Lista de exercícios sobre a área do triângulo

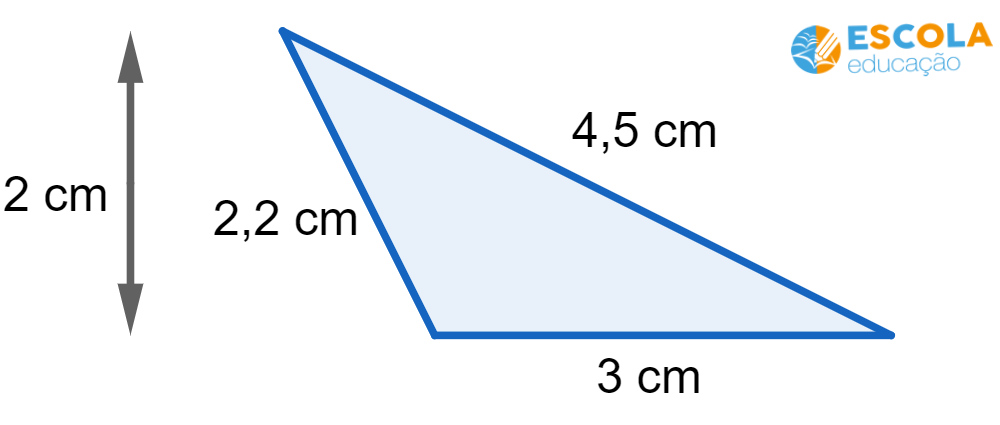
Questão 1. Determine a área de um triângulo com 2 cm de altura e medidas dos lados conforme a figura abaixo:

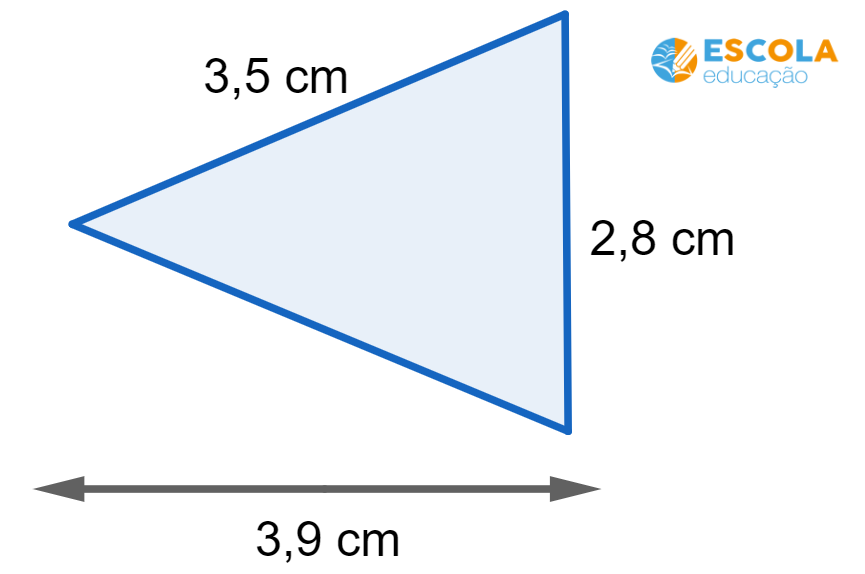
Questão 2. Calcule área do triângulo com as seguintes dimensões:

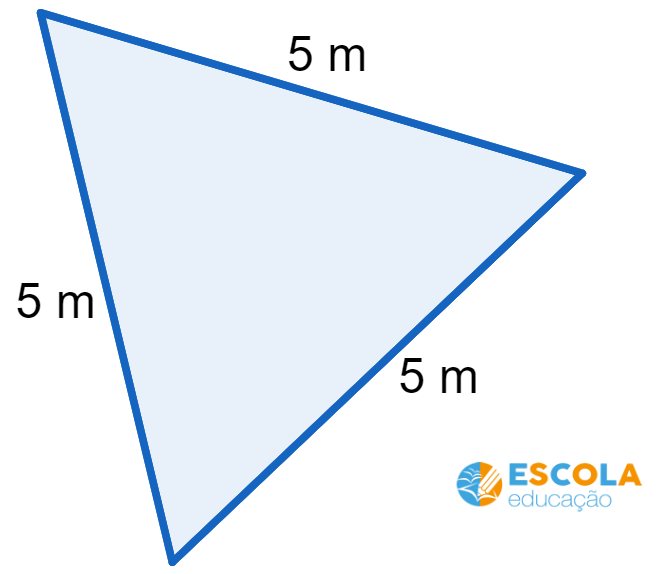
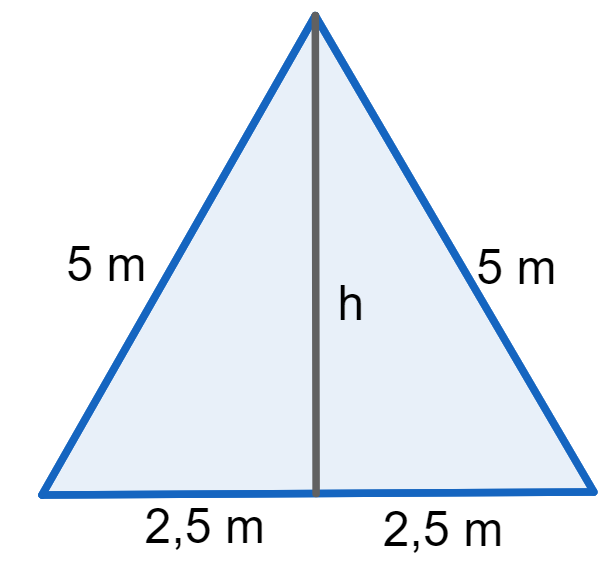
Questão 3. Calcule a área de um triângulo equilátero com 5 metros de lado.

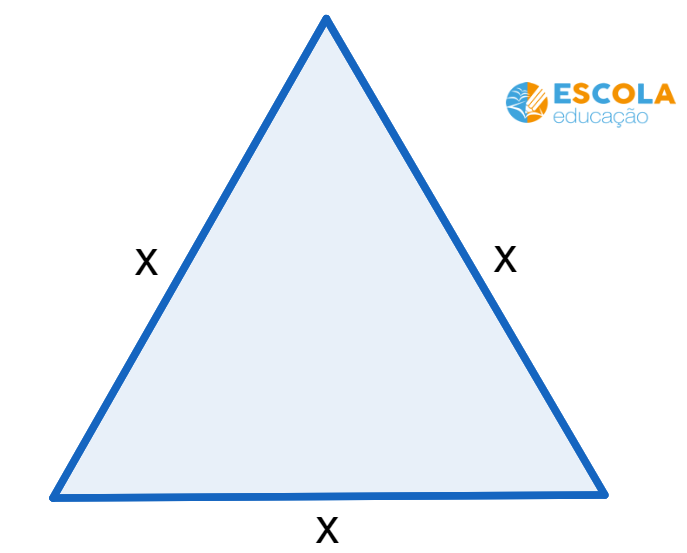
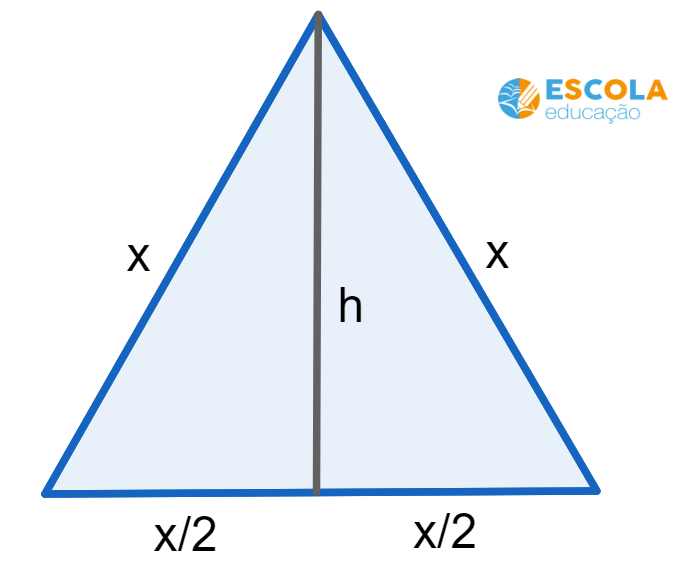
Questão 4. Um triângulo equilátero tem área igual a 15 cm². Qual a medida x dos lados desse triângulo?

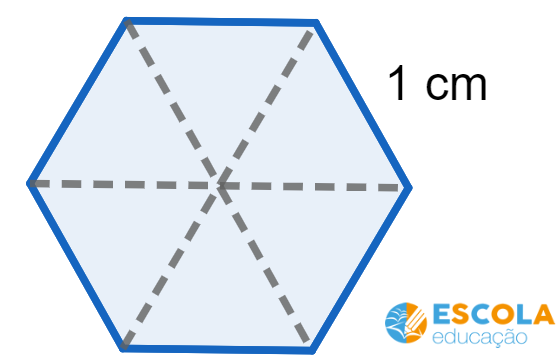
Questão 5. Calcule a área do hexágono regular apresentado na figura abaixo:

Resolução da questão 1

A altura do triângulo é igual a 2 cm e a base igual a 3 cm.

Assim, temos h = 2 e b = 3. Vamos aplicar esses valores na fórmula da área de um triângulo:

$\dpi{120} \mathrm{A = \frac{b\cdot h}{2}}$

$\dpi{120} \Rightarrow \mathrm{A = \frac{3\cdot 2}{2} = 3}$

Portanto, a área do triângulo é igual a 3 cm².

Lembre-se a área de uma figura geométrica é sempre uma medida quadrática, isto é, elevada ao quadrado.

Resolução da questão 2

A altura do triângulo é igual a 3,9 cm e a base igual a 2,8 cm.

Assim, temos h = 3,9 e b = 2,8. Vamos aplicar esses valores na fórmula da área de um triângulo:

$\dpi{120} \Rightarrow \mathrm{A = \frac{2,8\cdot 3,9}{2} = 5,46}$

Logo, a área do triângulo é igual a 5,46 cm².

Resolução da questão 3

Movendo o triângulo, podemos observar que a altura o divide em dois triângulos retângulos com cateto oposto igual a 2,5 metros.

Dessa forma, podemos utilizar o Teorema de Pitágoras para calcular a altura do triângulo:

$\dpi{120} \mathrm{h^2 =5^2 - (2,5)^2 }$

$\dpi{120} \Rightarrow \mathrm{h^2 =18,75 }$

$\dpi{120} \Rightarrow \mathrm{h \approx 4,32}$

Então, o triângulo tem aproximadamente 4,32 metros de altura. Com essa informação, já podemos calcular a área do triângulo equilátero:

$\dpi{120} \Rightarrow \mathrm{A \approx \frac{5\cdot 4,32}{2} = 10,8}$

Portanto, o triângulo equilátero tem em torno de 10,8 m² de área.

Resolução da questão 4

A altura divide o triângulo equilátero de lado x em dois triângulos retângulos com cateto oposto igual a x/2.

Pelo Teorema de Pitágoras, temos que:

$\dpi{120} \mathrm{h^2 =x^2 - \bigg(\frac{x}{2}\bigg)^2 }$

$\dpi{120} \Rightarrow \mathrm{h^2 =x^2 - \frac{x^2}{4}}$

$\dpi{120} \Rightarrow \mathrm{h^2 = \frac{3x^2}{4}}$

$\dpi{120} \Rightarrow \mathrm{h = \frac{x\sqrt{3}}{2}}$

Calculando a área do triângulo com b = x e $\dpi{120} \mathrm{h = \frac{x\sqrt{3}}{2}}$ , temos que:

$\dpi{120} \mathrm{A = \frac{x \cdot \frac{x\sqrt{3}}{2}}{2}}$

$\dpi{120} \mathrm{\Rightarrow A = \frac{x^2\sqrt{3}}{4}}$

Como temos a informação de que a área do triângulo deve ser igual a 15 cm², então:

$\dpi{120} \mathrm{ 15 = \frac{x^2\sqrt{3}}{4}}$

$\dpi{120} \mathrm{\Rightarrow x^2 = \frac{15\cdot 4}{\sqrt{3}}}$

$\dpi{120} \mathrm{\Rightarrow x \approx 5,88}$

Logo, a medida do lado do triângulo é aproximadamente igual a 5,88 cm.

Resolução da questão 5

A área do hexágono corresponde a soma das áreas dos seis triângulos formados pelas diagonais traçadas, conforme mostra a figura.

Assim, temos que calcular a área de um triângulo equilátero de lado 1 cm e depois multiplicar o resultado por 6.

Utilizando a fórmula da área de um triângulo equilátero encontrada no exercício anterior, temos que:

$\dpi{120} \mathrm{\Rightarrow A = \frac{1^2\sqrt{3}}{4} = \frac{\sqrt{3}}{4}}$

Então, a área do hexágono é dada por:

$\dpi{120} \mathrm{6\cdot A = 6\cdot \frac{\sqrt{3}}{4} \approx 2,6}$

Portanto, a área do hexágono é aproximadamente igual a 2,6 cm ².

Você também pode se interessar:

Exercícios de matemática resolvidos Exercícios sobre área de triângulos