Inequações – Primeiro e segundo grau

Aprenda a resolver inequações do 1° e 2° grau com exemplos simples e explicativos e saiba como utilizar os gráficos para encontrar as soluções.

Por Elainy Marciano Publicado em 15/04/2020 - 16:16

Uma inequação é uma sentença matemática que possui uma ou mais incógnitas e apresenta algum dos seguintes símbolos: > , < , ≥ ou ≤.

Exemplos de inequações:

Veja mais

O limite numérico: até onde vai o maior número que conhecemos?

Reditec debate ensino profissional e tecnológico

a) 3x + 4 > 1

b) 4y – 2y ≤ 8

Esses símbolos que aparecem nas inequações representam a existência de uma desigualdade, sendo que:

> → sinal de maior

< → sinal de menor

≥ → sinal de maior ou igual

≤ → sinal de menor ou igual

Inequação do primeiro grau

Chamamos de inequação do primeiro grau qualquer inequação onde o maior expoente da incógnita é 1.

Exemplos:

a) 5x – 3 > 2

b) 4x < -28

c) 5y ≥ 10

d) -3z + z ≤ 40

Resolução de uma inequação do primeiro grau

A resolução de uma inequação do 1° grau é feita de forma bem parecida com a de uma equação do 1° grau. Buscamos isolar a incógnita, trocando membros da inequação de lado, sempre que for preciso.

Exemplo: Resolver a inequação 7x + 6 > 4x + 7 para encontrar sua solução.

7x + 6 > 4x + 12

7x – 4x > 12 – 6

3x > 6

x > 6/3

x > 2

Assim, a solução dessa inequação é x > 2.

Contudo, quando a incógnita estiver multiplicada ou dividida por um número negativo e formos passar esse número para o outro lado da inequação, devemos multiplicar toda a inequação por (-1) e inverter o sinal da desigualdade.

Exemplo: Resolver a inequação 4x – 4 – 6x -2 ≤ 10 para encontrar sua solução.

4x – 4 – 6x -2 ≤ 10

4x – 6x ≤ 10 + 4 + 2

-2x ≤ 16 → Número negativo multiplicado por x e queremos passar para o outro lado

-2x ≤ 16 (-1) → Multiplicamos tudo por (-1) e invertemos a desigualdade

2x ≥ -16

x ≥ -16/2

x ≥ -8

Logo, a solução dessa inequação é x ≥ -8.

Resolução usando o gráfico da inequação

Uma outra forma de resolver uma inequação do 1° grau, é construindo um gráfico da equação da reta. Vamos ver como fazer isso através de um exemplo.

Exemplo: Encontrar a solução da inequação 10 – 9x ≥ 2x -1 utilizando o método gráfico.

1º passo) Passamos todos os termos pro lado esquerdo da inequação, deixando um zero no lado direito.

10 – 9x – 2x +1 ≥ 0

2° passo) Somamos os termos semelhantes.

10 – 9x – 2x +1 ≥ 0

-11x + 11 ≥ 0

É essa a inequação que vamos utilizar a partir de agora.

3° passo) Trocamos a desigualdade ≥ por uma igualdade (=) e resolvemos a equação para encontrar sua raiz.

-11x + 11 = 0

-11x = -11

x = -11/-11

x = 1

4° passo) Construímos o gráfico da equação da reta y = -11x + 11

Se o sinal da incógnita x for positivo, a reta é crescente.
Se o sinal da incógnita x for negativo, a reta é decrescente;

Então, nesse caso a reta é decrescente, já que o x está sendo multiplicado por um número negativo.

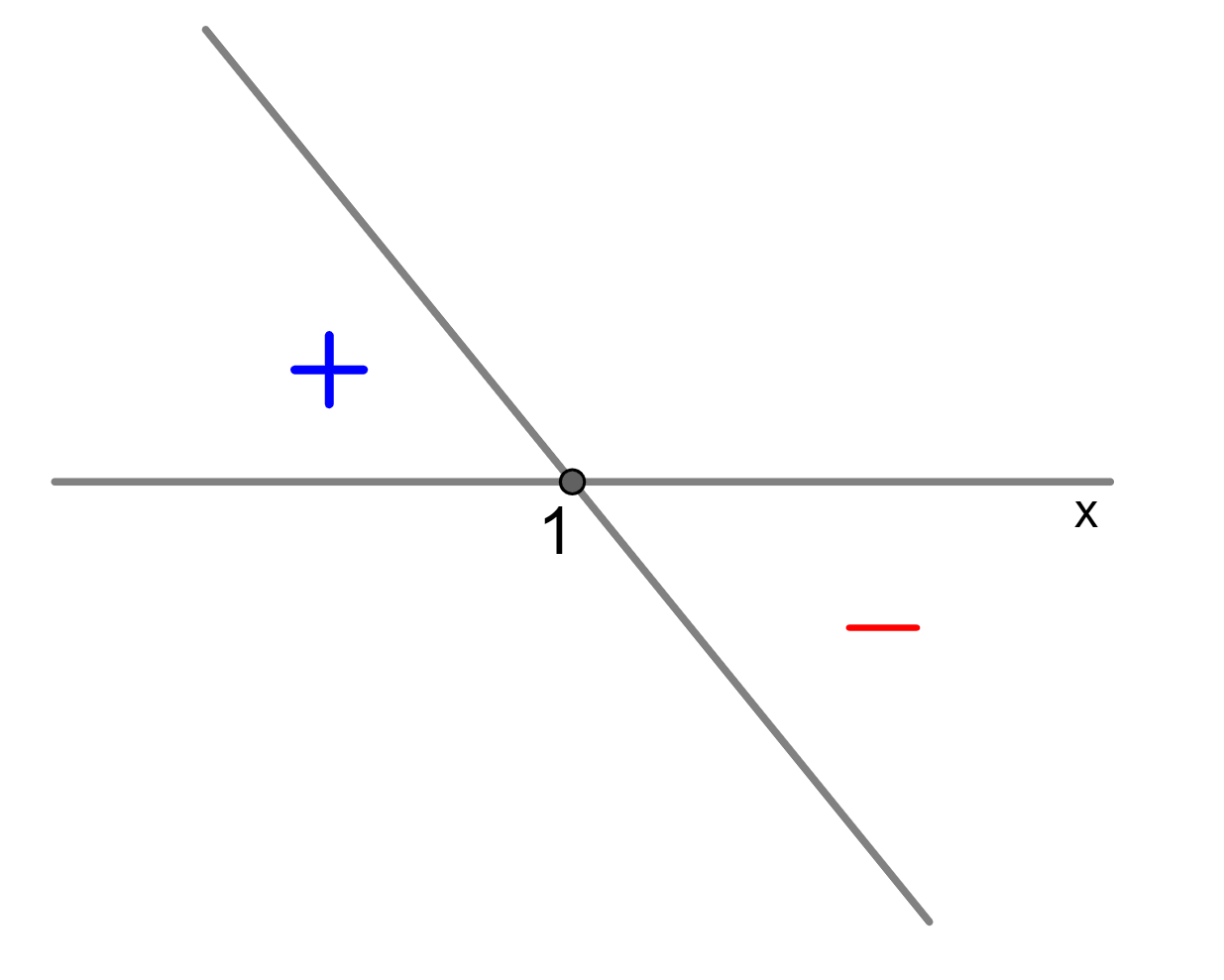
5° passo) Fazemos o estudo do sinal para determinar a solução da inequação.

y é igual a zero quando x é igual a 1.
y é maior que zero (+) quando x é menor que 1.
y é menor que zero (–) quando x é maior que 1.

A solução da inequação são os valores que tornam -11x + 11 ≥ 0 verdadeira, ou seja, os valores de x que levam a y ≥ 0 (y ser maior ou igual a zero).

Considerando o estudo de sinal, isso acontece quando x =1 e x <1, então a solução da inequação é x ≤ 1.

Inequação do segundo grau

Uma inequação do segundo grau é qualquer inequação onde o maior expoente da incógnita é 2.

Exemplos:

a) x² – 5x > 8

b) x² – 9 < 0

c) y² + y – 2 ≥ 0

d) 2y² + 5y ≤ -15

Para resolver uma inequação do segundo grau, utilizamos a fórmula de Bhaskara e fazemos o estudo de sinal da função, que nesse caso, será uma parábola.

Exemplo: Resolver a inequação x² + 3x – 4 > 0 para encontrar sua solução.

Trocamos a desigualdade > por uma igualdade e encontramos as raízes da equação:

x² + 3x – 4 = 0

Temos que:

$\flushleft \Delta = b^2 - 4 . a . c \\ \Delta = 3^2 - 4 . 1 . -6 \\ \Delta = 9 + 16 \\ \Delta = 25$

Então,

$x=\frac{-b\pm \sqrt{\Delta}}{2a} = \frac{-3 \pm \sqrt{25}}{2.1} = \frac{-3 \pm 5}{2}$

Assim, temos:

${x}' = \frac{-3+5}{2} = \frac{2}{2}=1 \: \: \: \textnormal{e}\: \: \: {x}'' = \frac{-3-5}{2} = \frac{-8}{2}=-4$

Portanto, as raízes da equação são 1 e – 4. Como x² tem sinal positivo na equação y = x² + 3x – 4, a parábola tem concavidade para cima.

Fazendo o estudo de sinal, poderemos observar que temos y > 0 quando x > 1 e quando x < -4. Logo, a solução da inequação x² + 3x – 4 > 0 é x > 1 e x < -4.

Você também pode se interessar: