Lei dos cossenos
A lei ou teorema dos cossenos possibilita determinar lados ou ângulos desconhecidos em qualquer triângulo. Entenda quando e como utilizar essa lei.
A lei dos cossenos, também conhecida por teorema dos cossenos, é composta por três diferentes equações que relacionam as medidas dos lados de qualquer triângulo aos seus ângulos.
É uma lei utilizada para determinar medidas desconhecidas de lados ou ângulos de triângulos.
Pela lei dos cossenos, o quadrado de cada lado é relacionado aos outros dois lados e ao cosseno do ângulo oposto ao lado, veja:
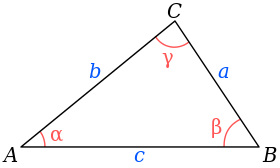
Lei dos cossenos:
a
Assim como a lei dos senos, a lei dos cossenos é válida para qualquer triângulo, mas, normalmente, é utilizada em triângulos oblíquos, como os apresentados a seguir:
No caso dos triângulos retângulos, existem relações específicas para determinar suas medidas, como o teorema de Pitágoras.
Aplicação da lei dos cossenos
Para aplicar a lei dos cossenos devemos conhecer dois lados do triângulo e o ângulo entre eles, ou conhecer os três lados do triângulo.
Exemplo (dois lados e um ângulo entre eles)
Dados os lados ,
e o ângulo
, encontre o valor do lado
.
Resolução:
Primeiro, determinamos o lado , pela lei dos cossenos:
Substituímos os valores conhecidos nessa equação:
Os outros ângulos podem ser determinados pela lei dos senos ou também pela lei dos cossenos, conforme o próximo exemplo.
Exemplo (três lados)
Dados os lados ,
e
, determine os ângulos internos do triângulo.
Resolução
Ângulo :
Ângulo :
Ângulo :
Em qualquer triângulo, a soma dos ângulos internos é igual a 180°, então, para descobrir o valor do último ângulo, nem precisamos utilizar a lei dos cossenos.
Temos que:
Você também pode se interessar:
- Funções trigonométricas – Seno, cosseno e tangente
- Lista de exercícios sobre semelhança de triângulos
- Classificação dos triângulos
- Lista de exercícios sobre a área do triângulo


Os comentários estão fechados, mas trackbacks E pingbacks estão abertos.