Lei dos senos
A lei dos senos serve para encontrar valores desconhecidos em qualquer tipo de triângulo. Entenda como utilizar essa lei e veja exemplos.
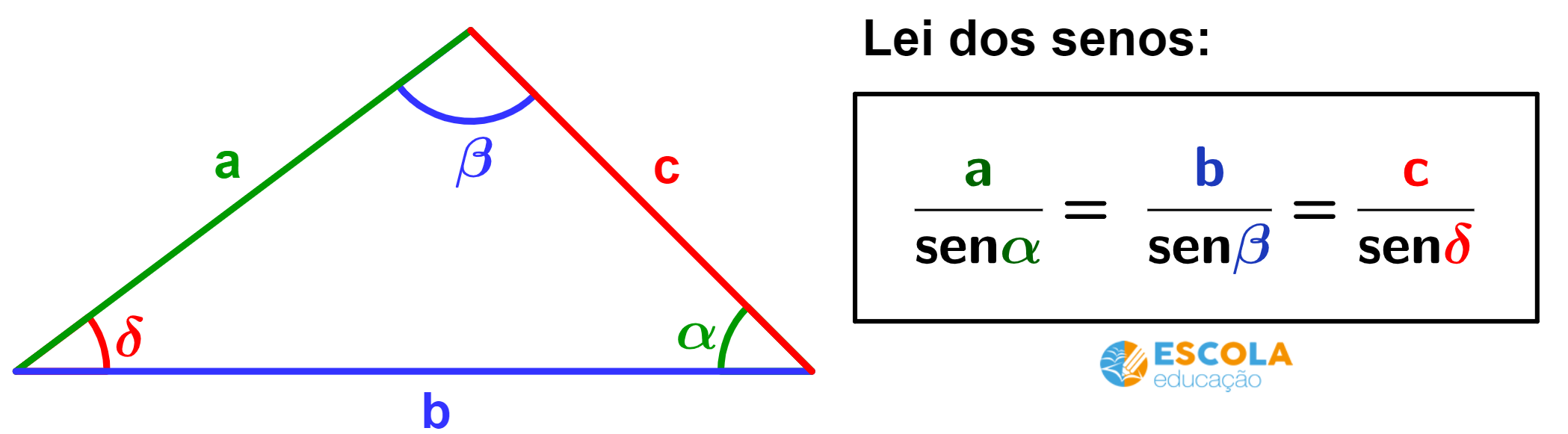
A lei dos senos ou teorema dos senos descreve uma relação que existe entre os lados e os ângulos de qualquer triângulo.
De acordo com a lei dos senos, a razão entre a medida do lado e do seno do ângulo oposto a esse lado é constante, ou seja, é o mesmo valor para os três lados do triângulo.
A lei dos senos é muito útil para resolver problemas que envolvem encontrar medidas de lados ou ângulos desconhecidos em triângulos que não são triângulos retângulos.
Em outras palavras, usamos a lei dos senos em triângulos acutângulos, que são os que possuem três ângulos agudos, ou em triângulos obtusângulos, que são aqueles com um ângulo obtuso e dois agudos.
Aplicação da lei dos senos
Para utilizar a lei dos senos precisamos conhecer pelo menos dois ângulos do triângulo e um de seus lados, ou então, dois lados e um ângulo oposto a um deles.
Exemplo (dois ângulos e um lado)
Dados os ângulos e
e o lado b = 120, encontre o valor do ângulo
e dos lados a e c.
Resolução:
Uma propriedade de qualquer triângulo é que a soma dos ângulos internos é igual a 180°.
Assim, sempre que tivermos dois ângulos, o terceiro pode ser encontrado de forma fácil.
Portanto, .
Pela lei dos senos, temos que:
Vamos determinar o valor do lado a através da seguinte proporção:
Pela propriedade fundamental das proporções, temos que:
Consultando os valores em uma tabela trigonométrica ou utilizando uma calculadora, verificamos que:
Portanto, o lado a mede aproximadamente 88,73 unidades de comprimento.
Para determinar o valor do lado c utilizamos a seguinte proporção:
Pela propriedade fundamental das proporções, temos que:
Portanto, o lado c mede aproximadamente 58,9 unidades de comprimento.
Exemplo (dois lados e um ângulo oposto)
Dados os lados a = 17 e b = 24 e o ângulo oposto , encontre o valor do lado c e dos ângulos
e
.
Resolução:
Pela lei dos senos, temos que:
Primeiro, vamos determinar o ângulo , utilizando a seguinte proporção:
Pela propriedade fundamental das proporções, temos que:
Agora, podemos encontrar o valor do ângulo :
Por fim, vamos calcular a medida do lado c:
Portanto, o lado c tem aproximadamente 23 unidades de comprimento.
Você também pode se interessar:
- Funções trigonométricas – Seno, cosseno e tangente
- Teorema de Pitágoras – História, fórmula, Triângulo Pitagórico
- Teorema de Tales
- Lista de exercícios sobre semelhança de triângulos


Os comentários estão fechados, mas trackbacks E pingbacks estão abertos.