O que é geometria analítica?

Geometria analítica é um campo de estudo da matemática que une geometria e álgebra, expressando as figuras geométricas a partir de expressões algébricas.

O título de pai ou criador da geometria analítica é atribuído a um filósofo, físico e matemático francês chamado René Descartes (1596-1650).

Na geometria analítica, vários conceitos muitas vezes abstratos podem ser compreendidos com mais clareza a partir de um sistema de coordenadas, chamado de plano cartesiano.

O plano cartesiano é formado por duas retas perpendiculares, chamadas de eixos. O ponto de encontro entre as retas é o ponto (0,0), ele é chamado de origem. A partir daí qualquer outro ponto pode ser localizado, bastando conhecer as suas coordenadas (x, y).

Em resumo, geometria analítica utiliza o sistema de coordenadas para descrever de forma algébrica as figuras geométricas, expressar distâncias, pontos de intersecção, posições de retas, ângulos de inclinação, áreas, volumes, entre outros.

Exemplo: 

A reta é uma figura geométrica bem simples, ela é formada por infinitos pontos alinhados e possui uma única dimensão.

Apesar dela ser infinita nos dois sentidos, representar uma reta no papel é fácil, basta fazer um traço sem curvatura.

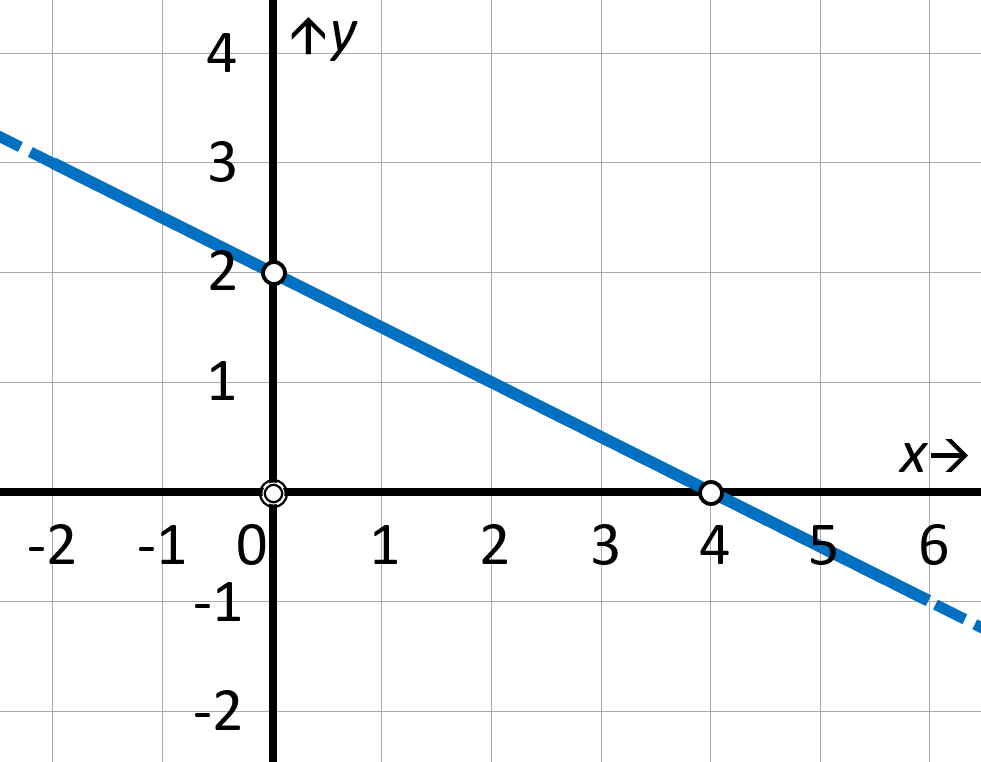
Além disso, toda reta pode ser representada por uma equação e seus pontos podem ser localizados no plano cartesiano.

Na figura a seguir, está representada a reta cuja equação é .

Você também pode se interessar:

• Geometria Plana
• Geometria Espacial
• Equação do 2° Grau
• Diferenças entre função e equação
• Circunferência – Definição, características e equação reduzida