Lista de exercícios de polígonos

Os polígonos fazem parte do estudo de geometria plana, podendo ser classificados em diferentes tipos, como: simples, complexos, regulares, côncavos, convexos, etc.

Além disso, existem muitas fórmulas relacionadas ao estudo dos polígonos. Podemos estar interessados no número de diagonais, na soma dos ângulos internos ou externos, entre outras medidas.

Por isso, para você tirar suas dúvidas e ficar fera nesse assunto, preparamos uma lista com 10 exercícios resolvidos sobre polígonos. Veja!

Lista de exercícios de polígonos

---

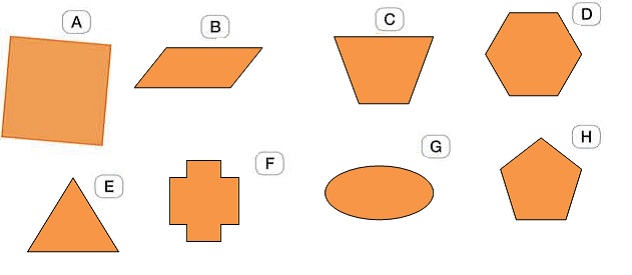
Questão 1. Identifique qual das figuras abaixo não se classifica como um polígono. Justifique sua resposta.

---

Questão 2. Marque V para verdadeiro e F para falso.

a) (  ) Um polígono é chamado de côncavo quando possui todos os lados iguais e todos os ângulos internos de mesma medida.

b) (  ) Um polígono é regular quando possui lados congruentes e ângulos internos congruentes.

c) (  ) Um polígono é denominado convexo quando qualquer segmento de reta, com extremidades em seu interior, não possui pontos fora dele.

d) (  ) O número de vértices em um polígono simples é sempre menor que o número de lados.

e) (  ) As diagonais de um polígono são segmentos de reta que ligam dois vértices quaisquer de um polígono.

---

Questão 3. Qual a medida da soma dos ângulos internos e externos de um pentadecágono convexo?

---

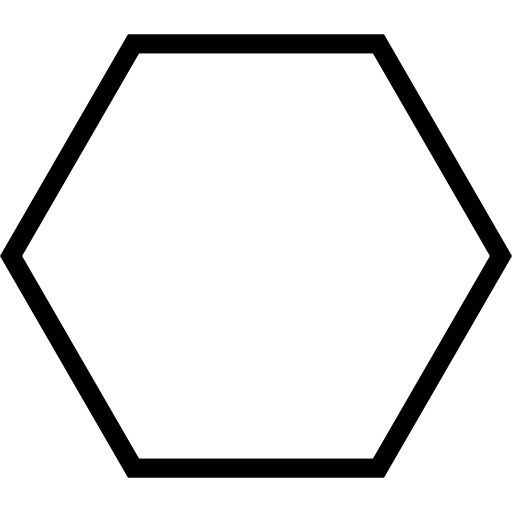
Questão 4. Determine a medida de cada ângulo interno do polígono regular abaixo:

---

Questão 5. Qual o nome do polígono que tem 44 diagonais?

---

Questão 6. Determine o número de lados de um polígono cuja soma dos seus ângulos internos é igual a soma dos seus ângulos externos.

---

Questão 7. Determine o número de lados de um polígono sabendo que o seu número de diagonais é igual ao triplo do seu número de lados.

---

Questão 8. Calcule o valor da soma dos ângulos internos de um polígono sabendo que o seu número de diagonais é igual a oito vezes o seu número de lados.

---

Questão 9. Descubra quantos lados tem um polígono equiângulo cuja soma das medidas de oito ângulos internos é igual a 1296°.

---

Questão 10. Os lados de um polígono regular medem 5 cm cada um. Se a medida do seu perímetro for igual ao número de diagonais, qual a medida da soma dos ângulos internos desse polígono?

---

Resolução da questão 1

Letra G.

A figura da letra G é formada por uma linha curva, arrendondada, enquanto os polígonos devem ser formados apenas por segmentos de reta.

Resolução da questão 2

a) F, essa é a definição de polígono regular.

b) V

c) V

d) F, o número de vértices é igual ao número de lados.

e) F, os vértices devem ser não consecutivos, ou seja, o segmento deve passar pelo meio do polígono para ser uma diagonal.

Resolução da questão 3

A soma dos ângulos internos de qualquer polígono convexo é igual a 360°.

Já a soma dos ângulos internos é dada pela seguinte fórmula:

S = (n – 2) . 180

Onde n é o número de lados.

Assim, no pentadecágono, temos que:

S = (n – 2) . 180

S = (15 – 2) . 180

S = 13 . 180

S = 2340

Então, a soma dos ângulos internos do pentadecágono é 2340°.

Resolução da questão 4

Em um polígono regular, todos os ângulos internos têm a mesma medida. Para obter a medida de cada ângulo, basta dividir a soma das medidas dos ângulos internos por n.

A soma das medidas dos ângulos internos nesse polígono, que é um hexágono, é:

S = (n – 2) . 180

S = (6 – 2) . 180

S = 4 . 180

S = 720

Dividindo esse valor por n = 6, temos que cada ângulo interno mede 120°.

Resolução da questão 5

Para saber o nome do polígono, temos que saber quantos lados ele tem.

A informação que temos é que o número de diagonais é igual a 44, ou seja:

[n(n – 3) / 2] = 44

Resolvendo, podemos encontrar o valor de n:

[n(n – 3) / 2] = 44

n(n – 3) = 44 . 2

n² – 3n = 88

n² – 3n – 88 = 0

Utilizando a fórmula de Bhaskara, podemos encontrar dois valores para n:

n = 11 ou n = – 8

Como n é o número de lados, portanto, é um número positivo, temos que o número de lados desse polígono é igual a 11. Logo, o nome dele é undecágono.

Resolução da questão 6

A soma dos ângulos internos de um polígono é dada por (n – 2) . 180, onde n é o número de lados do polígono. Já a soma dos ângulos internos de um polígono é 360°.

Assim, se essas duas medidas são iguais, temos que:

(n – 2) . 180 = 360

Resolvendo, podemos encontrar o valor de n:

(n – 2) . 180 = 360

180n – 360 = 360

180n = 360 + 360

180n = 720

n = 720/180

n = 4

Portanto, esse polígono tem quatro lados.

Resolução da questão 7

O número de diagonais de um polígono é dado por: [n(n – 3) / 2]. Se essa quantidade é igual ao triplo do número de lados, temos que:

[n(n – 3) / 2] = 3n

Cancelando n dos dois lados da equação, temos:

(n – 3) / 2 = 3

(n – 3) = 3 . 2

n – 3 = 6

n = 6 + 3

n = 9

Logo, o polígono possui nove lados.

Resolução da questão 8

Para calcular a soma dos ângulos internos de um polígono, precisamos saber o número de lados.

Pelas informações dadas, temos que:

[n(n – 3) / 2] = 8n

Cancelando n dos dois lados da equação, temos:

(n – 3) / 2 = 8

(n – 3) = 8 . 2

n – 3 = 16

n = 16 + 3

n = 19

Agora, vamos utilizar a fórmula da soma dos ângulos internos:

(n – 2) . 180 =

(19 – 2) . 180 =

17 . 180 =

3060

Assim, a soma dos ângulos internos desse polígono é igual a 3060°.

Resolução da questão 9

Um polígono equiângulo é um polígono onde todos os seus ângulos internos têm a mesma medida.

Nesse tipo de polígono, a medida de um ângulo interno pode ser obtida quando dividimos a soma das medidas dos ângulos internos pelo número de lados n.

Ou seja,

[(n – 2) . 180] / n

Se oito ângulos internos somam juntos 1296°, então:

8. [(n – 2) . 180] / n = 1296

Resolvendo:

8. [(n – 2) . 180] / n = 1296

8. [(n – 2) . 180] = 1296n

8 [180n – 360] = 1296n

1440n – 2880 = 1296n

1440n – 1296n = 2880

144n = 2880

n = 2880/144

n = 20

Logo, o número de lados do polígono é igual a 20.

Resolução da questão 10

Em um polígono regular com n lados, o perímetro é dado pela multiplicação de n pela medida do lado. Assim, se o lado mede 5 cm, temos que o perímetro é igual a 5n.

Se o perímetro desse polígono é igual ao número de diagonais, temos que:

[n(n – 3) / 2] = 5n

Cancelando n dos dois lados e resolvendo:

(n – 3) / 2 = 5

n – 3 = 5 . 2

n – 3 = 10

n = 10 + 3

n = 13

Sabendo o número de lados, já podemos calcular a soma das medidas dos ângulos internos:

(n – 2) . 180 =

(13 – 2) . 180 =

11 . 180 =

1980

Então, a soma das medidas dos ângulos internos desse polígono é igual a 1980°.

Você também pode se interessar:

• Área e perímetro
• Áreas de figuras planas
• Lista de exercícios de potenciação
• Lista de exercícios de área de figuras planas
• Lista de exercícios de expressões numéricas