Retas perpendiculares

Aprenda sobre as retas perpendiculares e saiba qual é a condição de perpendicularidade entre duas retas.

Por Elainy Marciano Publicado em 17/08/2020 - 06:42

Retas perpendiculares são duas retas que possuem um ponto de intercepto, no qual se forma um ângulo reto (ângulo de 90°).

Desse modo, retas perpendiculares são um caso particular de retas concorrentes.

Veja mais

O limite numérico: até onde vai o maior número que conhecemos?

Reditec debate ensino profissional e tecnológico

Existe uma condição que permite identificar quando duas retas são ou não perpendiculares. Essa condição é baseada no valor do coeficiente angular de cada reta.

Condição de perpendicularidade

Uma reta r com coeficiente angular $\dpi{120} \boldsymbol{m_1}$ e uma reta s com coeficiente angular $\dpi{120} \boldsymbol{m_2}$ são perpendiculares quando:

$\dpi{120} \boldsymbol{m_1\cdot m_2= -1}$

Ou seja, quando multiplicamos os valores dos coeficientes angulares, o resultado deve ser igual a -1 para que as retas sejam perpendiculares.

Observe que essa condição também pode ser expressa como $\dpi{120} m_1 = -\frac{1}{m_2}$ ou $\dpi{120} m_2 = -\frac{1}{m_1}$ . As três formas são equivalentes.

Demonstração

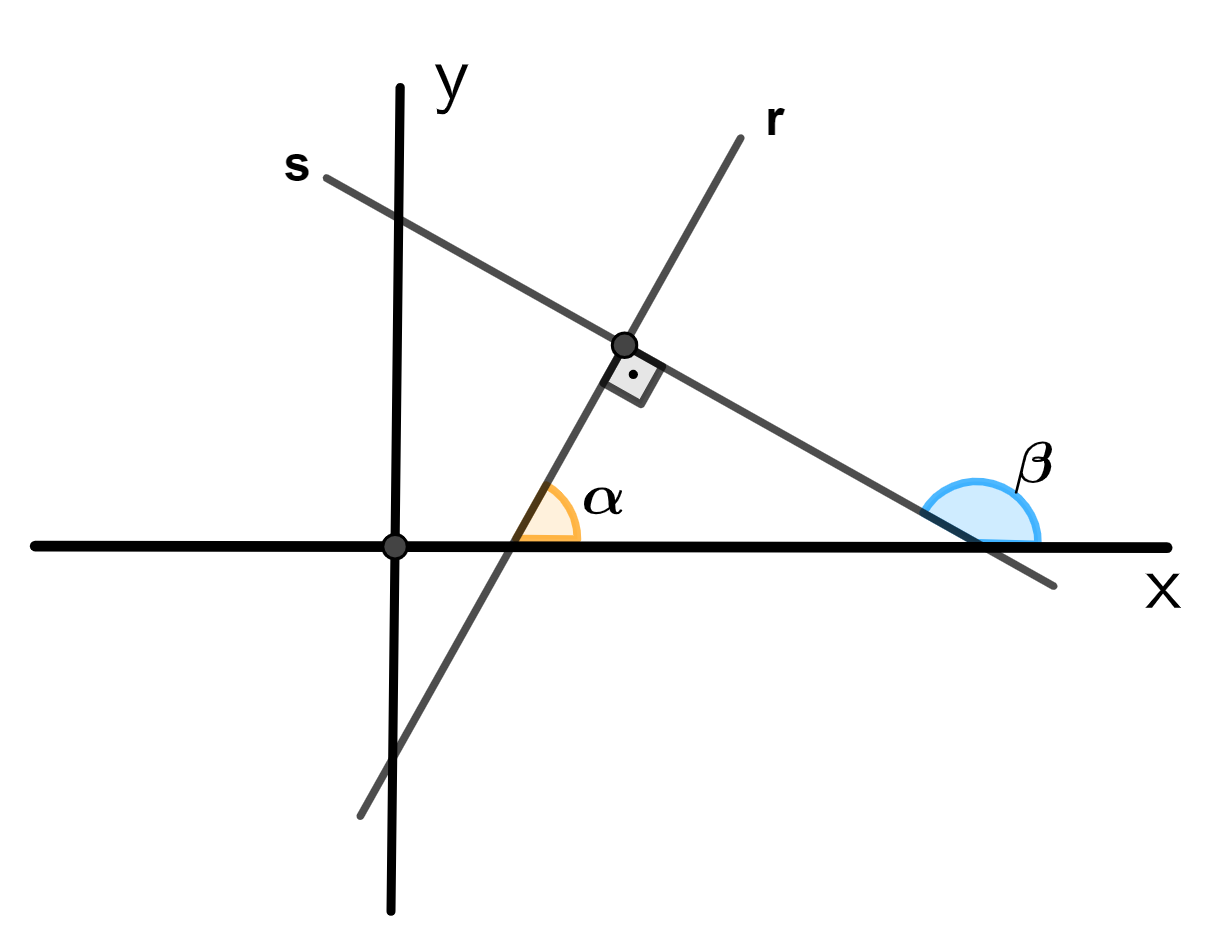
Podemos mostrar que essa condição é verdadeira, considerando que r e s sejam perpendiculares e que o ângulo de inclinação da reta r é $\dpi{120} \alpha$ e o ângulo de inclinação da reta s é $\dpi{120} \beta$ .

No triângulo formado na figura, temos um ângulo reto (90°), um ângulo $\dpi{120} \alpha$ e um terceiro ângulo que é o suplemento do ângulo $\dpi{120} \beta$ .

Chamando esse terceiro ângulo de $\dpi{120} \gamma$ , temos que $\dpi{120} \gamma = 180^{\circ} - \beta$ .

Como em qualquer triângulo, a soma dos três ângulos internos é sempre igual a 180° e já temos um ângulo de 90°, a soma dos ângulos $\dpi{120} \alpha$ e $\dpi{120} \gamma$ deve ser igual a 90°. Dessa forma temos:

$\dpi{120} \alpha + \gamma = 90^{\circ}$

$\dpi{120} \alpha + (180^{\circ}- \beta) = 90^{\circ}$

$\dpi{120} \beta = \alpha +90^{\circ}$

Aplicando a tangente dos dois lados da equação, temos que:

$\dpi{120} tan\, \beta = tan(\alpha +90^{\circ})$

Considerando as razões trigonométricas, temos que:

$\dpi{120} tan(\alpha+90^{\circ}) = \frac{sen(\alpha+90^{\circ})}{cos(\alpha+90^{\circ})}$

Por essas duas últimas equações, temos que:

$\dpi{120} tan \, \beta = \frac{sen(\alpha+90^{\circ})}{cos(\alpha+90^{\circ})}$

Aplicando as relações de seno e cosseno da soma de dois ângulos, temos que:

$\dpi{120} tan \, \beta = \frac{sen\, \alpha.cos\, 90^{\circ}+sen\, 90^{\circ}.cos\, \alpha}{cos\alpha.cos\, 90^{\circ}-sen\, \alpha.sen\, 90^{\circ}}$

Como seno de 90° é 1 e cosseno de 90° é 0, temos que:

$\dpi{120} tan \, \beta = -\frac{cos \alpha}{sen \alpha}= -\frac{1}{tan \alpha}$

O coeficiente angular é definido como a tangente do ângulo de inclinação, assim, temos $\dpi{120} m_1 = tan\, \alpha$ e $\dpi{120} m_2 = tan\, \beta$ .

Dessa forma, podemos escrever:

$\dpi{120} m_2 = -\frac{1}{m_1}$

$\dpi{120} \Rightarrow m_1\cdot m_2 = -1$

Você também pode se interessar: