Soma dos ângulos internos de um triângulo

Os triângulos são polígonos de três lados e possuem três ângulos internos. Entre os ângulos internos de um triângulo, existe uma relação muito importante:

Relação entre as medidas dos ângulos internos de um triângulo

Vamos mostrar duas formas diferentes de verificar a relação que existe entre os ângulos internos de um triângulo.

1ª forma:

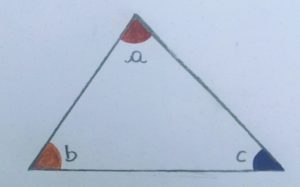
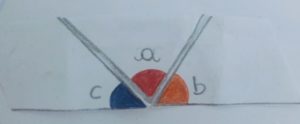
Considere o desenho de um triângulo qualquer, com ângulos internos a, b e c. Se juntarmos os três vértices, perceberemos que os ângulos formam um ângulo de meia volta, ou seja, de 180°.

Faça o teste você mesmo, desenhando diferentes tipos de triângulos e observando que essa relação sempre será verdadeira.

2ª forma:

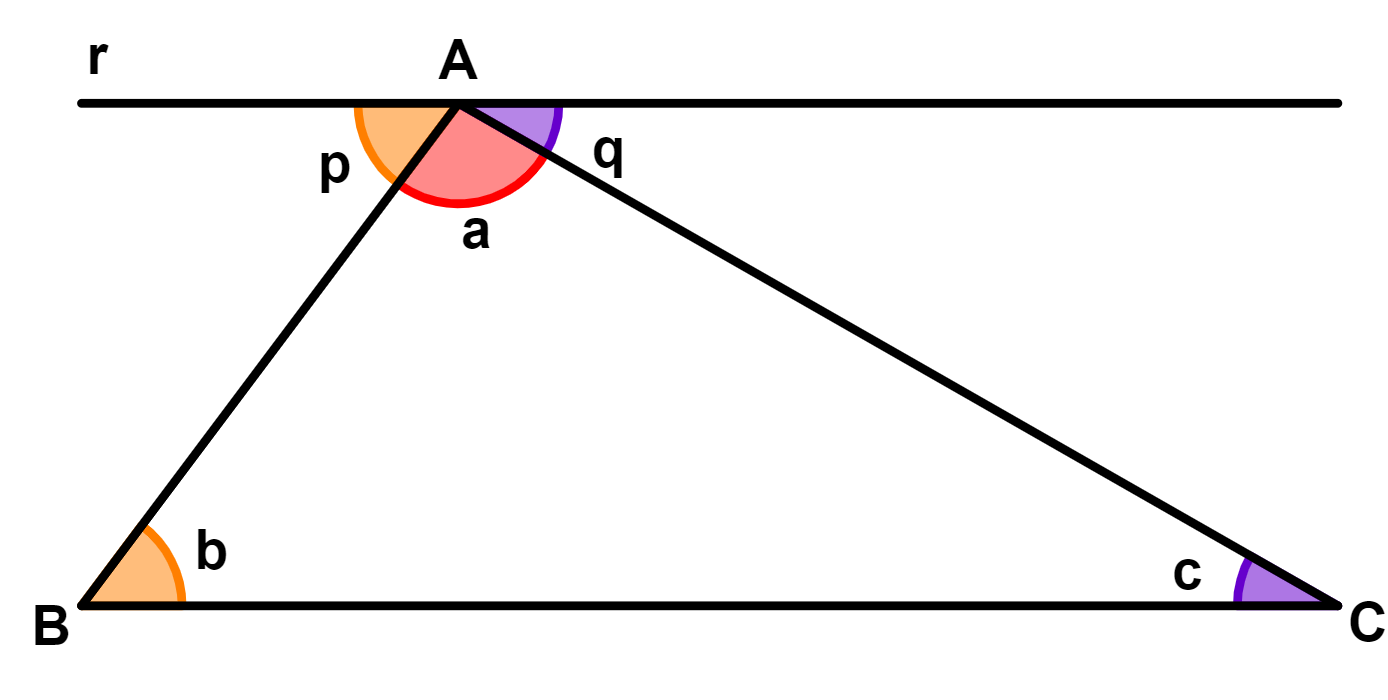
Outra forma de verificar a relação que existe entre os ângulos internos de um triângulo é traçando uma reta que passe por um dos vértices do triângulo e que seja paralela ao lado oposto a esse vértice, como na figura abaixo:

Observe que, ao traçar a reta r, paralela ao lado BC, obtém-se dois ângulos externos, p e q. Veja que, com o ângulo a, os ângulos p e q formam um ângulo de meia volta, então:

a + p + q = 180°

Uma vez que a reta r e o lado BC são paralelos, se enxergarmos o lado AB e o lado AC como retas transversais, veremos que os ângulos p e b e os ângulos q e c são pares de ângulos alternos internos.

Uma propriedade muito importante dos ângulos alternos internos formados por retas paralelas, é que eles possuem a mesma medida, são congruentes, ou seja:

p = b e q = c

Assim, substituindo p por b e q por c na equação acima, temos que:

a + b + c = 180°

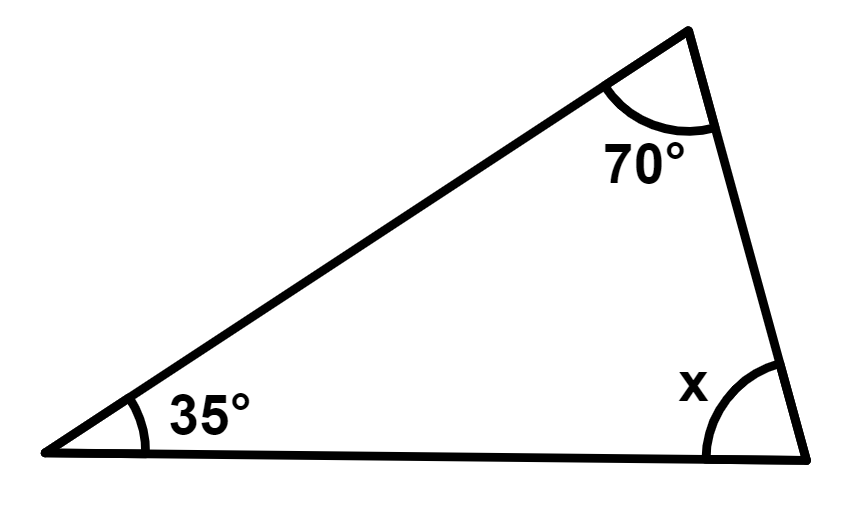
Exemplo 1: Determine o valor de x na figura abaixo:

Pela relação entre os ângulos internos de um triângulo, temos que:

70° + 35° + x = 180°

Trata-se de uma equação do 1º grau, então, vamos isolar x:

x = 180° – 70° – 35°

⇒ x = 75°

Exemplo 2: Determine a medida do terceiro ângulo interno dos triângulos com os seguintes ângulos:

a) 30° e 45°

Como a soma dos três ângulos deve ser igual a 180°, então, para saber o terceiro ângulo basta subtrair de 180° a medida dos outros dois ângulos que foram dados.

180° – 30° – 45° = 105°

Portanto, o terceiro ângulo mede 105°.

b) 100° e 50°

180° – 100° – 50° = 30°

Portanto, o terceiro ângulo mede 30°.

c) 90° e 28°

180° – 90° – 28° = 62°

Portanto, o terceiro ângulo mede 62°.

Você também pode se interessar:

• Congruência de triângulos
• Condição da existência de um triângulo
• Área do triângulo usando os ângulos
• Baricentro de um triângulo